
分析 (1)当S6=20时,即回答6个问题后,正确4个,错误2个.若回答正确第1个和第2个问题,则其余4个问题可任意回答正确2个问题;若第一个问题回答正确,第2个问题回答错误,第三个问题回答正确,则其余三个问题可任意回答正确2个.记回答每个问题正确的概率为p,则$p=\frac{2}{3}$,同时回答每个问题错误的概率为$\frac{1}{3}$,由此能求出S6=20且Si≥0(i=1,2,3)的概率.
(2)由X=|S5|可知X的取值为10,30,50,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)当S6=20时,即回答6个问题后,正确4个,错误2个.
若回答正确第1个和第2个问题,则其余4个问题可任意回答正确2个问题;
若第一个问题回答正确,第2个问题回答错误,第三个问题回答正确,则其余三个问题可任意回答正确2个.
记回答每个问题正确的概率为p,则$p=\frac{2}{3}$,同时回答每个问题错误的概率为$\frac{1}{3}$…(3分)
故所求概率为:$P={({\frac{2}{3}})^2}×C_4^2×{({\frac{2}{3}})^2}×{({\frac{1}{3}})^2}+\frac{2}{3}×\frac{1}{3}×\frac{2}{3}×C_3^2×{({\frac{2}{3}})^2}×\frac{1}{3}=\frac{16}{81}$…(6分)
(2)由X=|S5|可知X的取值为10,30,50
可有$P({X=10})=C_5^3{({\frac{2}{3}})^3}{({\frac{1}{3}})^2}+C_5^2{({\frac{2}{3}})^2}{({\frac{1}{3}})^3}=\frac{40}{81}$,
$P({X=30})=C_5^4{({\frac{2}{3}})^4}{({\frac{1}{3}})^1}+C_5^1{({\frac{2}{3}})^1}{({\frac{1}{3}})^4}=\frac{30}{81}$,
$P({X=50})=C_5^5{({\frac{2}{3}})^5}+C_5^0{({\frac{1}{3}})^5}=\frac{11}{81}$…(9分)
故X的分布列为:
| X | 10 | 30 | 50 |
| P | $\frac{40}{81}$ | $\frac{30}{81}$ | $\frac{11}{81}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
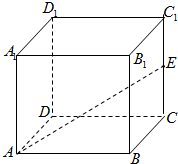 如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)
如图,已知正方体ABCD-A1B1C1D1,AA1=2,E为棱CC1的中点,则AE与平面B1BCC1所成的角为$arctan\frac{{2\sqrt{5}}}{5}$.($arcsin\frac{2}{3}$,$arccos\frac{{\sqrt{5}}}{3}$)(结果用反三角表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{13}}{4}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | -$\frac{\sqrt{3}}{4}$ | D. | -$\frac{\sqrt{13}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
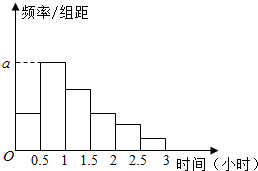 随着智能手机等电子产品的普及,“低头族”正成为现代社会的一个流行词.在路上、在餐厅里、在公交车上,随处可见低头玩手机的人,这种“低头族现象”冲击了人们面对面交流的温情,也对人们的健康构成一定的影响.为此,某报社发起一项专题调查,记者随机采访了M名市民,得到这M名市民每人在一天内低头玩手机的时间(单位:小时),根据此数据作出频数的统计表和频率分布直方图如下:
随着智能手机等电子产品的普及,“低头族”正成为现代社会的一个流行词.在路上、在餐厅里、在公交车上,随处可见低头玩手机的人,这种“低头族现象”冲击了人们面对面交流的温情,也对人们的健康构成一定的影响.为此,某报社发起一项专题调查,记者随机采访了M名市民,得到这M名市民每人在一天内低头玩手机的时间(单位:小时),根据此数据作出频数的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [0,0.5) | 4 | 0.10 |
| [0.5,1) | m | p |
| [1,1.5) | 10 | n |
| [1.5,2) | 6 | 0.15 |
| [2,2.5) | 4 | 0.10 |
| [2.5,3) | 2 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $3\sqrt{2}$ | C. | $2+\frac{{\sqrt{2}}}{2}$ | D. | $1+\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com