
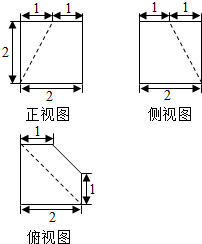
分析 由三视图得到该截面为如图所示的梯形BDEF,共中E,F分别是棱D1C1、B1C1的中点,由此能求出该截面的面积.
解答 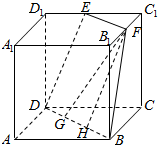 解:由 一个棱长为2的正方体被一个平面截去一部分后,剩余部分的三视图,
解:由 一个棱长为2的正方体被一个平面截去一部分后,剩余部分的三视图,
得到该截面为如图所示的梯形BDEF,共中E,F分别是棱D1C1、B1C1的中点,
取DB中点G,BG中点H,连结FG、FH,
由已知得EF=$\sqrt{2}$,BD=2$\sqrt{2}$,EF$\underset{∥}{=}$DG,∴DEFG是平行四边形,∴DE=BF=FG=$\sqrt{4+1}$=$\sqrt{5}$,
∴FH⊥BD,且FG=$\sqrt{5-\frac{1}{2}}$=$\sqrt{\frac{9}{2}}$,
∴该截面的面积为S=$\frac{\sqrt{2}+2\sqrt{2}}{2}×\sqrt{\frac{9}{2}}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查截面面积的求法,考查简单空间图形的三视图,是基础题,解题时要认真审题,注意空间思维能力的培养.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,2) | C. | [2,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 年 份 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 人口总数y | 8 | 8 | 8 | 9 | 9 | 10 | 11 |
| A. | (3,9) | B. | (9,3) | C. | (6,14) | D. | (4,11) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
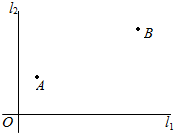 如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.
如图,在A,B两城周边有两条直线互相垂直的高速公路l1,l2,在点O外交汇,A城到高速公路l1,l2的距离分别是30km,20km,B城到高速公路l1,l2的距离分别是60km,80km,为了方便居民出行,现要在高速公路l1或l2上建造一个高速公路出入口P(不能建造在点O处),经调查,若出入口O建造在高速公路l1上,A,B两城居民的“不满意度”M1=$\frac{1}{2}$(PA+PB),若出入口P建造在高速公路l2上,A,B两城居民的“不满意度”M2=$\frac{1}{2}$$\sqrt{P{A}^{2}+P{B}^{2}}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com