选修4-4：坐标系与参数方程
已知在直角坐标平面内，以坐标原点
为极点，
轴的正半轴为极轴，建立极坐标系，点
的极坐标是
,曲线
的极坐标方程为
.
（1）求点 的直角坐标和曲线的直角坐标方程；
（2）若经过点的直线
与曲线交于
两点，求
的最小值.
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案科目：高中数学 来源：2016届海南师范大学附属中学高三临考模拟数学试卷（解析版） 题型：解答题
选修4-1：几何证明选讲
如图，直线
经过⊙
上一点
，⊙
的半径为
，
是等腰三角形，且
是
中点，⊙ 交直线
于
.
（Ⅰ）证明：直线
与⊙相切；
（Ⅱ）若
的正切值为
，求
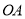的长.
查看答案和解析>>
科目：高中数学 来源：2016届福建省高三下学期周考六理科数学试卷（解析版） 题型：选择题
已知
是双曲线
：
上的一点，
是
上的两个焦点，若
，则
的取值范围是（ ）
A．
B．
C．
D．
查看答案和解析>>
科目：高中数学 来源：2016届安徽师大附中高三最后一卷理科数学试卷（解析版） 题型：解答题
2014年12月初，南京查获了一批问题牛肉，滁州市食药监局经民众举报获知某地
个储存牛肉的冷库有
个冷库牛肉被病毒感染，需要通过对库存牛肉抽样化验病毒
来确定感染牛肉，以免民众食用有损身体健康.下面是两种化验方案：方案甲：逐个化验样品，直到能确定感染冷库为止.方案乙：将样品分为两组，每组三个，并将它们混合在一起化验，若存在病毒,则表明感染牛肉在这三个样品当中，然后逐个化验，直到确定感染冷库为止；若结果不含病毒，则在另外一组样品中逐个进行化验.
（1）求依据方案乙所需化验恰好为
次的概率.
（2）首次化验化验费为
元，第二次化验化验费为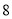
元，第三次及其以后每次化验费都是
元，列出方案甲所需化验费用的分布列，并估计用方案甲平均需要化验费多少元？
（3）试比较两种方案，估计哪种方案有利于尽快查找到感染冷库.说明理由.
查看答案和解析>>
科目：高中数学 来源：2016届江西省高三第三次模拟文科数学试卷（解析版） 题型：解答题
已知函数
，
.
（1）当
时，求函数
在
上的单调区间；
（2）若函数存在两个极值点，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
， 
，
是边
上的点（包括端点），则
的取值范围是（ ）
B．
C．
D．
中任取
个不同的数，则取出的
个数之差的绝对值为
的概率是（ ）
B．
C．
D．
，设实数
满足约束条件：
，
，则
的取值范围为（ ）
B．
D．
是定义在
上的偶函数，且对于任意的
,满足
,若当
,
，则函数 
在区间
上的零点个数为 ．