
已知二次函数
(1)若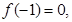 试判断函数
试判断函数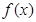 零点个数;
零点个数;
(2)若对任意的 ,且
,且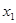 <
< ,
, (
( >0),试证明:
>0),试证明:
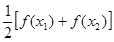 >
>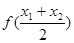 成立。
成立。
(3)是否存在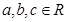 ,使
,使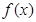 同时满足以下条件:①对任意
同时满足以下条件:①对任意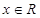 ,
, ,且
,且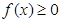 ②对任意的
②对任意的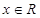 ,都有
,都有 ?若存在,求出
?若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
(1) 零点为1个或2个;(2)见解析;(3) 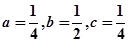 。
。
【解析】
试题分析:(1)∵f(-1)=0,∴a-b+c=0即b=a+c,故△=b2-4ac=(a+c)2-4ac=(a-c)2,
当a=c时,△=0,函数f(x)有一个零点;当a≠c时,△>0,函数f(x)有两个零点.
(2)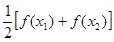 -
-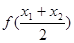 =
=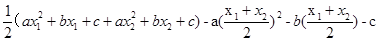
=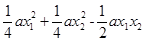 =
=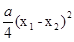
因为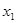 <
<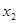 ,
,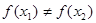 (
(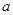 >0)所以
>0)所以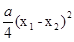 >0,即
>0,即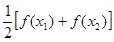 -
-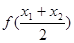 >0,
>0,
所以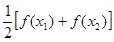 >
>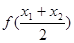 成立。
成立。
(3)假设存在a,b,c满足题设,由条件①知抛物线的对称轴为x=-1且f(x)min=0;∴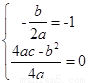 即
即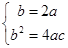 ,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,∴f(1)=1,即a+b+c=1,由
,所以a=c,在条件②中令x=1,有0≤f(1)-1≤0,∴f(1)=1,即a+b+c=1,由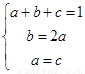 得
得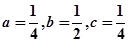 ,所以存在
,所以存在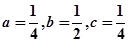 使f(x)同时满足条件①②。
使f(x)同时满足条件①②。
考点:本题考查函数的零点与方程根的关系。
点评:本题考查函数零点个数与方程根的个数问题,以及存在性问题的处理方式,属于较难的题目.主要分析思路(1)通过对二次函数对应方程的判别式进行分析判断方程根的个数,从而得到零点的个数;(2)存在性问题的一般处理方法就是假设存在,然后根据题设条件求得参数的值.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| n |
 |
| i=2 |
| lnai |
| ai2 |
| 2n2-n-1 |
| 4(n+1) |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年河北省高三第一次调研考试理科数学试卷(解析版) 题型:解答题
对于函数 ,若存在
,若存在 ,使
,使 ,则称
,则称 是
是 的一
的一
个"不动点".已知二次函数
(1)当 时,求函数
时,求函数 的不动点;
的不动点;
(2)对任意实数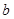 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求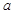 的取值范围;
的取值范围;
(3)在(2)的条件下,若 的图象上
的图象上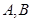 两点的横坐标是
两点的横坐标是 的不动点,
的不动点,
且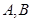 两点关于直线
两点关于直线 对称,求
对称,求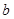 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2011-2012年广东省高一上学期11月月考数学 题型:解答题
(本题满分12分)
已知二次函数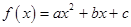
(1)若 ,试判断函数
,试判断函数 零点个数
零点个数
(2) 若对 且
且 ,
, ,证明方程
,证明方程 必有一个实数根属于
必有一个实数根属于
(3)是否存在 ,使
,使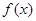 同时满足以下条件①当
同时满足以下条件①当 时, 函数
时, 函数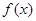 有最小值0;;②对
有最小值0;;②对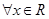 ,都有
,都有 。若存在,求出
。若存在,求出 的值,若不存在,请说明理由。
的值,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com