练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某景点拟建一个扇环形状的花坛（如图所示），按设计要求扇环的周长为36米，其中大圆弧所在圆的半径为14米，设小圆弧所在圆的半径为米，圆心角为（弧度）.

    ⑴ 求关于的函数关系式；

    ⑵ 已知对花坛的边缘（实线部分）进行装饰时，直线部分的装饰费用为4元/米，弧线部分的装饰费用为16元/米，设花坛的面积与装饰总费用之比为，求关于的函数关系式，并求出的最大值.

    【答案】⑴⑵ 的最大值为

    【解析】试题分析：（1）根据扇形的周长公式进行求解即可．
    （2）结合花坛的面积公式，结合费用之间的关系进行求解即可．

    试题解析：

    ⑴由题可知，

    所以.

    ⑵花坛的面积为，

    装饰总费用为，

    所以花坛的面积与装饰总费用之比为，

    令， ，

    则，

    当且仅当取等号，此时， ，

    故花坛的面积与装饰总费用之比为，

    且的最大值为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数 (其中为自然对数的底数).

    （1）当时，求函数的单调递增区间；

    （2）若函数在区间上单调递减，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，则输出的k的值为（ ）

    A.7
    B.6
    C.5
    D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥E﹣ABCD中，平面EAD⊥平面ABCD，DC∥AB，BC⊥CD，且AB=4，BC=CD=ED=EA=2．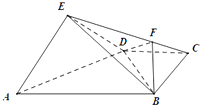
    （1）求二面角E﹣AB﹣D的正切值；
    （2）在线段CE上是否存在一点F，使得平面EDC⊥平面BDF？若存在，求 的值，若不存在请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， 分别是椭圆： （）的左、右焦点，离心率为， ， 分别是椭圆的上、下顶点， ．

    （1）求椭圆的方程；

    （2）过作直线与交于， 两点，求三角形面积的最大值（是坐标原点）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线在点处的切线与曲线也相切.

    (1)求实数的值；

    (2)设函数，若且，证明: .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如下图的程序框图，如果输入的，则输出的（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数列中. ,

    （Ⅰ）求的通项公式；

    （Ⅱ）求数列的前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列4个命题

    ①“若，则”的否命题是“若，则”；

    ②若命题，则为真命题；

    ③“平面向量夹角为锐角，则”的逆命题为真命题；

    ④“函数有零点”是“函数在上为减函数”的充要条件.

    其中正确的命题个数是（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    同步练习册答案