
分析 (1)由已知结合数列递推式分别取n=2,n=3求得a3,a4的值,构造${b}_{n}={{a}_{n}}^{2}-{a}_{n-1}{a}_{n+1}$,作差说明bn+1=bn,结合${b}_{2}={{a}_{2}}^{2}-{a}_{1}{a}_{3}=-500$说明?n≥2,n∈N+,${{a}_{n}}^{2}$-an-1•an+1恒为定值;
(2)由(1)知,-500=${{a}_{n}}^{2}$-an-1•an+1=${{a}_{n}}^{2}-(3{a}_{n}-{a}_{n+1}){a}_{n+1}={{a}_{n}}^{2}-3{a}_{n}{a}_{n+1}$$+{{a}_{n+1}}^{2}$,两边同加501+5an•an+1得,$5{a}_{n+1}{a}_{n}+1=({a}_{n}+{a}_{n+1})^{2}+501$.构造数列
cn=5an+1an,要使cn为完全平均数,则?m∈Z,满足${c_n}={m^2}$,记dn=an+an+1,可得$501={m^2}-d_n^2=(m+{d_n})(m-{d_n})$,结合501=3×167=1×501,得到关于m与dn的方程组,求解方程组得到m与dn的值,再结合{cn}为单调递增数列得答案.
解答 解:(1)当n=2时,a3=3a2-a1=70,
当n=3时,a4=3a3-a2=180,…
构造${b}_{n}={{a}_{n}}^{2}-{a}_{n-1}{a}_{n+1}$,
${b}_{n+1}-{b}_{n}={{a}_{n+1}}^{2}-{a}_{n}{a}_{n+2}-{{a}_{n}}^{2}$$+{a}_{n-1}{a}_{n+1}={{a}_{n+1}}^{2}-{a}_{n}(3{a}_{n+1}-{a}_{n})$$-{{a}_{n}}^{2}+(3{a}_{n}-{a}_{n+1}){a}_{n+1}$=0.
又${b}_{2}={{a}_{2}}^{2}-{a}_{1}{a}_{3}=-500$,
∴?n≥2,n∈N+,bn=-500.
即?n≥2,n∈N+,${{a}_{n}}^{2}$-an-1•an+1恒为定值;
(2)由(1)知,-500=${{a}_{n}}^{2}$-an-1•an+1=${{a}_{n}}^{2}-(3{a}_{n}-{a}_{n+1}){a}_{n+1}={{a}_{n}}^{2}-3{a}_{n}{a}_{n+1}$$+{{a}_{n+1}}^{2}$,
两边同加501+5an•an+1得,$5{a}_{n+1}{a}_{n}+1=({a}_{n}+{a}_{n+1})^{2}+501$.
不妨令cn=5an+1an,要使cn为完全平均数,则?m∈Z,满足${c_n}={m^2}$,
记dn=an+an+1,则$501={m^2}-d_n^2=(m+{d_n})(m-{d_n})$,
又501=3×167=1×501,
则有$\left\{\begin{array}{l}{m-{d}_{n}=1}\\{m+{d}_{n}=501}\end{array}\right.$或$\left\{\begin{array}{l}{m-{d}_{n}=3}\\{m+{d}_{n}=167}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=251}\\{{d}_{n}=250}\end{array}\right.$或$\left\{\begin{array}{l}{m=85}\\{{d}_{n}=82}\end{array}\right.$.
即${c}_{n}=25{1}^{2}$或${c}_{n}=8{5}^{2}$,又数列{cn}为单调递增数列,可求:
${c}_{1}=3001<8{5}^{2},{c}_{2}=10501>8{5}^{2}$,${c}_{3}=63001=25{1}^{2}$.
故满足条件的n的集合为{3}.
点评 本题考查数列递推式,考查逻辑思维能力和推理论证能力,题目(2)的设置,灵活性强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
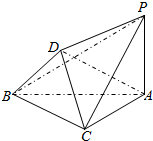 如图,在多面体PABCD中,△ABC是边长为2的正三角形,BD=DC=$\sqrt{3}$,AD=$\sqrt{5}$,PA⊥平面ABC.
如图,在多面体PABCD中,△ABC是边长为2的正三角形,BD=DC=$\sqrt{3}$,AD=$\sqrt{5}$,PA⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
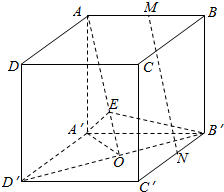 如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.
如图,在正方体ABCD-A′B′C′D'′中,O是B′D′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)
如图,已知四边形ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3,PB的中点E,求异面直线AE与PC所成角的大小.(用反三角表示)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com