
分析 (1)假设设h(x+T)=T•h(x)进而得出结论;
(2)通过设g(x+T)=T•g(x)并令x=0可知T=$\frac{1}{2}$,分T>$\frac{1}{2}$、T<$\frac{1}{2}$两种情况证明唯一性即可;
(3)利用f(n+2)=2•f(n)及f(1)=1、f(2)=-4分别计算出n为奇数、偶数时的值,进而利用等比数列的求和公式计算可知S2n=-3(2n-1)、S2n-1=-2n+3,计算即得结论.
解答 (1)结论:h(x)=x不是T倍周期函数.
理由如下:
依题意,设h(x+T)=T•h(x),则x+T=T•x对任意x恒成立,
∵T无解,
∴h(x)=x不是T倍周期函数;
(2)证明:设g(x+T)=T•g(x),则$(\frac{1}{4})^{x+T}$=T•$(\frac{1}{4})^{x}$对任意x恒成立,
令x=0,得$(\frac{1}{4})^{T}$=T,即T=$\frac{1}{2}$;
下证唯一性:
若T>$\frac{1}{2}$,T=$(\frac{1}{4})^{T}$<$(\frac{1}{4})^{\frac{1}{2}}$=$\frac{1}{2}$,矛盾;
若T<$\frac{1}{2}$,T=$(\frac{1}{4})^{T}$>$(\frac{1}{4})^{\frac{1}{2}}$=$\frac{1}{2}$,矛盾;
∴T=$\frac{1}{2}$是唯一的;
(3)解:依题意,f(3)=f(1+2)=2f(1)=2,
f(5)=f(3+2)=2f(3)=22,
f(7)=f(5+2)=2f(5)=23,
…
f(2n-1)=f(2n-3+2)=2f(2n-3)=2n-1,
∴f(1)+f(3)+…f(2n-1)=1+2+22+…+2n-1=2n-1,
同理可得:f(2)+f(4)+…+f(2n)=-4(1+2+22+…+2n-1)=-4(2n-1),
∴S2n=f(1)+f(2)+…+f(2n)=-3(2n-1),
同理S2n-1=f(1)+f(2)+…+f(2n-1)=-2n+3,
∴$\underset{lim}{n→∞}$Cn=$\underset{lim}{n→∞}$$\frac{{S}_{2n}}{{S}_{2n-1}}$=$\underset{lim}{n→∞}$$\frac{3({2}^{n}-1)}{{2}^{n}-3}$=3.
点评 本题考查数列的求和与极限,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
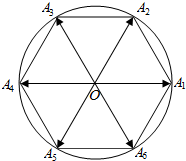 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1(x>2)$ | C. | y2=8x | D. | y2=8x(x≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点A、B分别是角α、β的终边与单位圆的交点,$0<β<\frac{π}{2}<α<π$.
如图,点A、B分别是角α、β的终边与单位圆的交点,$0<β<\frac{π}{2}<α<π$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com