
分析 由a3=2,a7=1求出等差数列{$\frac{1}{{a}_{n}+1}$}的公差,再代入通项公式求出$\frac{1}{{a}_{n}+1}$,可求出a1.
解答 解:因为数列{$\frac{1}{{a}_{n}+1}$}是等差数列,且a3=2,a7=1,
所以$\frac{1}{{a}_{7}+1}$=$\frac{1}{2}$,$\frac{1}{{a}_{3}+1}$=$\frac{1}{3}$,$\frac{1}{{a}_{7}+1}$-$\frac{1}{{a}_{3}+1}$=$\frac{1}{6}$,
设{$\frac{1}{{a}_{n}+1}$}公差为d,则4d=$\frac{1}{6}$,故d=$\frac{1}{24}$,
所以$\frac{1}{{a}_{n}+1}$=$\frac{1}{{a}_{3}+1}$+(n-3)d=$\frac{1}{3}$+(n-3)×$\frac{1}{24}$=$\frac{n+5}{24}$,
故an=$\frac{19-n}{n+5}$,
所以a1=$\frac{19-1}{1+5}$=3.
故答案是:3.
点评 本题考查等差数列的性质、通项公式的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a+2c<2 | B. | 2-a<2c | C. | a<0,b≥0,c>0 | D. | a<0,b<0,c<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
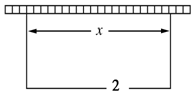 围建一个面积为300m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长,利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为75元/m,新墙的造价为150元/m,设利用的旧墙的长度为xm(x>0).
围建一个面积为300m2的矩形场地,要求矩形场地的一面利用旧墙(旧墙足够长,利用旧墙需维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为75元/m,新墙的造价为150元/m,设利用的旧墙的长度为xm(x>0).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com