解:(1)∵向量
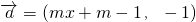
,
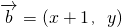
,m∈R,且

∴[m(x+1)-1](x+1)-y=0 2’
y=f(x)=mx
2+(2m-1)x+m-1 4’
(2)由题意A,B是△ABC的两个内角
∴tanC=-tan(A+B)
∵tanA,tanB是方程f(x)+2=0的两个实根
∴
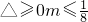
8’
tanA+tanB=
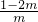
,tanAtanB=
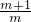
∴
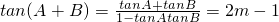
∴tanC=1-2m 9’
A,B是三角形的内角,至多一个为钝角,tanA,tanB中至多有一个取负值,且都不为零
若都为正,由韦达定理tanA+tanB=
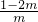
>0,得

,又
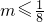
,可得
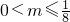
,故有tanC=1-2m
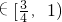
10’
若一正一负,由韦达定理tanAtanB=
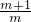
<0,可得-1<m<0,故有tanC∈(1,3)11’
综上
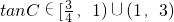
12’
分析:(1)由题意,
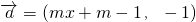
,
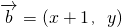
,m∈R,且

,利用内积为0可得出关于y与x的方程,再用x表示出y即可得到函数y=f(x);
(2)由于tanC=-tan(A+B),结合公式
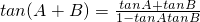
及tanA,tanB是方程f(x)+2=0的两个实根利用根与系数的关系即可将tanC用m表示出来,再由题设条件求出m的取值范围,即可求出tanC的取值范围
点评:本题考点是平面向量的综合题,考查了数量积的运算,正切的和角公式,根与系数的关系等,解题的关键是理解题意,将问题正确转化,本题的难点是对参数取值范围的讨论,易因为没有考虑方程两根tanA,tanB的符号导致扩大了范围,产生错误,解题时要注意通盘考虑题词设中的限制条件,等价转化,考察了转化的思想方程的思想及分类讨论的思想,本题综合性强,难度较大,有一个严谨做题的好习惯可避免出错

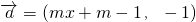 ,
,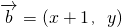 ,m∈R,且
,m∈R,且
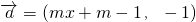 ,
,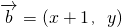 ,m∈R,且
,m∈R,且
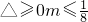 8’
8’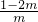 ,tanAtanB=
,tanAtanB=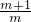
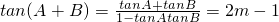
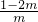 >0,得
>0,得 ,又
,又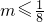 ,可得
,可得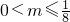 ,故有tanC=1-2m
,故有tanC=1-2m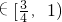 10’
10’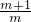 <0,可得-1<m<0,故有tanC∈(1,3)11’
<0,可得-1<m<0,故有tanC∈(1,3)11’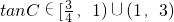 12’
12’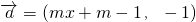 ,
,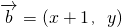 ,m∈R,且
,m∈R,且 ,利用内积为0可得出关于y与x的方程,再用x表示出y即可得到函数y=f(x);
,利用内积为0可得出关于y与x的方程,再用x表示出y即可得到函数y=f(x);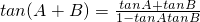 及tanA,tanB是方程f(x)+2=0的两个实根利用根与系数的关系即可将tanC用m表示出来,再由题设条件求出m的取值范围,即可求出tanC的取值范围
及tanA,tanB是方程f(x)+2=0的两个实根利用根与系数的关系即可将tanC用m表示出来,再由题设条件求出m的取值范围,即可求出tanC的取值范围

 春雨教育同步作文系列答案
春雨教育同步作文系列答案 ,其中向量
,其中向量 ,
, ,x∈R,且y=f(x)的图象经过点
,x∈R,且y=f(x)的图象经过点 .
. sin2x如何变换得到?
sin2x如何变换得到?