已知动点P(x,y)与两定点M(-1,0),N(1,0)连线的斜率之积等于常数λ(λ≠0).
(1)求动点P的轨迹C的形状;
(2)试根据λ的取值情况讨论轨迹C的形状;
(3)当λ=-2时,过E(1,0)作两条互相垂直直线l1、l2,且分别与轨迹C交于A、B两点,探究直线AB是否过定点?若过定点,请求出定点坐标;否则,说明理由.
解:(1)由题设知直线PM与PN的斜率存在且均不为零
所以
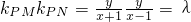
,
整理得
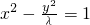
(λ≠0,x≠±1)(3分)
(2)①当λ>0时,轨迹C为中心在原点,焦点在x轴上的双曲线(除去顶点)
②当-1<λ<0时,轨迹C为中心在原点,焦点在x轴上的椭圆(除去长轴两个端点)
③当λ=-1时,轨迹C为以原点为圆心,1的半径的圆除去点(-1,0),(1,0)
④当λ<-1时,轨迹C为中心在原点,焦点在y轴上的椭圆(除去短轴的两个端点)(7分)
(3)当λ=-2时,轨迹C的椭圆
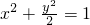
(x≠±1)
由题意知,l
1的斜率存在
设l
1的方程为y=k(x-1),设l
2的方程为y=-

(x-1),
将l
1的方程代入椭圆方程中整理得
(x-1)[(k
2+2)x-k
2]=0(*)
设A(x
1,y
1),B(x
2,y
2),则x
1,x
2的方程(*)的两个实根,
则x
1=

,∴y
1=
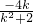
,即A(

,
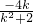
),
同理,得B(
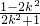
,
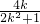
),
∴直线AB的斜率为k
AB=
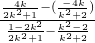
=
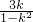
(k≠±1)
∴直线AB的方程为:y+
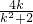
=
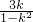
(x-

),
化简得:y=
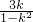
(x+

),它恒过点(-

,0)
k=±1时,直线AB也过点(-

,0).
∴直线AB过点(-

,0).(13分).
分析:(1)由题设知直线PM与PN的斜率存在且均不为零,所以
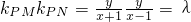
,由此能够导出动点P的轨迹C的方程.
(2)当λ>0时,轨迹C为中心在原点,焦点在x轴上的双曲线(除去顶点);当-1<λ<0时,轨迹C为中心在原点,焦点在x轴上的椭圆(除去长轴两个端点);当λ=-1时,轨迹C为以原点为圆心,1的半径的圆除去点(-1,0),(1,0);当λ<-1时,轨迹C为中心在原点,焦点在y轴上的椭圆(除去短轴的两个端点).
(3)当λ=-2时,轨迹C的椭圆
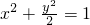
(x≠±1),由题意知,由题意知,l
1的斜率存在,设l
1的方程为y=k(x-1),设l
2的方程为y=-

(x-1),代入椭圆方程中整理得(x-1)[(k
2+2)x-k
2]=0,由此入手能够求出直线AB的方程,最后根据直线的方程得出它过定点.
点评:本题考查直线和圆锥曲线的综合运用,解题时要认真审题,注意分类讨论思想和均值不等式的合理运用.

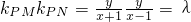 ,
,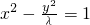 (λ≠0,x≠±1)(3分)
(λ≠0,x≠±1)(3分)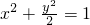 (x≠±1)
(x≠±1) (x-1),
(x-1), ,∴y1=
,∴y1=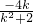 ,即A(
,即A( ,
,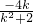 ),
),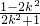 ,
,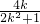 ),
),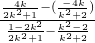 =
=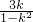 (k≠±1)
(k≠±1)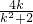 =
=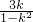 (x-
(x- ),
),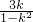 (x+
(x+ ),它恒过点(-
),它恒过点(- ,0)
,0) ,0).
,0). ,0).(13分).
,0).(13分).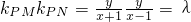 ,由此能够导出动点P的轨迹C的方程.
,由此能够导出动点P的轨迹C的方程.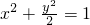 (x≠±1),由题意知,由题意知,l1的斜率存在,设l1的方程为y=k(x-1),设l2的方程为y=-
(x≠±1),由题意知,由题意知,l1的斜率存在,设l1的方程为y=k(x-1),设l2的方程为y=- (x-1),代入椭圆方程中整理得(x-1)[(k2+2)x-k2]=0,由此入手能够求出直线AB的方程,最后根据直线的方程得出它过定点.
(x-1),代入椭圆方程中整理得(x-1)[(k2+2)x-k2]=0,由此入手能够求出直线AB的方程,最后根据直线的方程得出它过定点.
