练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-7，已知在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，过D点作⊙O的切线交AC于E.

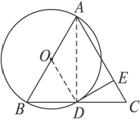
    图2-7

    求证：（1）DE⊥AC；

    （2）BD2=CE·CA.

    思路分析:本例是考查切线的性质与直径所对的圆周角是直角的综合题，掌握常见的辅助线作法是解题关键，即连结圆心和切点的半径，根据切线的性质，则有半径垂直于这条切线.

    证明:(1)连结OD、AD.

    ∵DE是⊙O的切线，D为切点，

    ∴OD⊥DE.

    ∵AB是⊙O的直径，

    ∴AD⊥BC.∴AB=AC，BD=DC.

    ∴OD∥AC，DE⊥AC.

    (2)∵AD⊥BC，DE⊥AC，

    ∴△CDE∽△CAD.

    ∴.∴CD2=CE·CA.

    ∴BD=DC.∴BD2=CE·CA.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设定义在[-1，7]上的函数y=f（x）的图象如图所示．已知（a，b）是y=
    2012
    f(x)
    +2012    的一个单调递增区间，则b-a的最大值为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

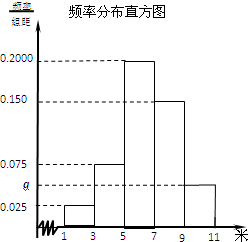    精英家教网为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11）五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
    （1）求实数a的值及参加“掷铅球”项目测试的人数；
    （2）若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试，求所抽取的2名学生自不同组的概率．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年重庆市三峡名校联盟高三12月联考文科数学试卷（解析版） 题型：解答题

    (本小题满分13分)为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．

    (1)求实数的值及参加“掷铅球”项目测试的人数；

    (2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试，求所抽取的2名学生自不同组的概率．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

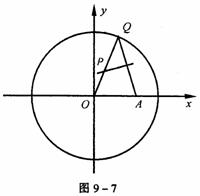
    如图9-7，已知圆C：x2+y2=4,A(,0)是圆内一点。Q是圆上一动点，AQ的垂直平分线交OQ于P，当点Q在圆C上运动一周时，点P的轨迹为曲线E。

    （1）求曲线E的方程；

    （2）过点O作倾斜角为θ的直线与曲线E交于B1、B2两点，当θ在范围（0，）内变化时，求△AB1B2的面积S(θ)的最大值。

    查看答案和解析>>

    同步练习册答案