考点:数列的应用,利用导数研究曲线上某点切线方程
专题:综合题,等差数列与等比数列
分析:(Ⅰ)通过求导即可得到切线的斜率,进而得到切线的方程,即可得到x
n+1与x
n的关系,利用等比数列的通项公式即可求出.
(Ⅱ)求出
SPnQnQnPn+1=
(+)(2n+1-2n)=
,
SPn+1Qn+1Qn+1Pn+2=
,
SPnQnQn+2Pn+2=
,即可求出三角形P
nP
n+1P
n+2的面积为定值.
解答:
解:(Ⅰ)由
y=求导得
y′=-,
∴曲线C:
y=在点P(1,1)处的切线方程为y-1=-(x-1),即y=-x+2.
此切线与x轴的交点Q
1的坐标为(2,0),
∴点P
1的坐标为
(2,).即
x1=2,y1=.-------------------(2分)
∵点P
n的坐标为(x
n,y
n)(n∈N
*),P
n在曲线C上,所以
yn=,
∴曲线C:
y=在点P
n(x
n,y
n)处的切线方程为
y-=-(x-xn),---(5分)
令y=0,得点Q
n+1的横坐标为x
n+1=2x
n.
∴数列{x
n}是以2为首项,2为公比的等比数列.
∴
xn=2n(n∈N
*).---------------------(8分)
(Ⅱ)设P
n(x
n,y
n),P
n+1(x
n+1,y
n+1),P
n+2(x
n+2,y
n+2),
∵
SPnQnQnPn+1=
(+)(2n+1-2n)=
,
SPn+1Qn+1Qn+1Pn+2=
,
SPnQnQn+2Pn+2=
,
∴△P
nP
n+1P
n+2的面积为
--=
.
点评:熟练掌握导数的几何意义、等比数列的通项公式及其前n项和公式,三角形面积计算公式是关键.

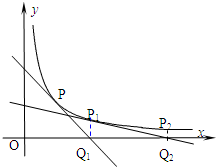 如图,已知曲线C:y=
如图,已知曲线C:y=

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 如图所示:m个实数a1,a2,…,am,(m≥3,m∈N)依次按顺时针方向围成一个圆圈.
如图所示:m个实数a1,a2,…,am,(m≥3,m∈N)依次按顺时针方向围成一个圆圈.