

| C | 0 1 |
| 1 |
| 2 |
| C | 0 2 |
| 1 |
| 2 |
| C | 1 1 |
| 1 |
| 2 |
| C | 0 2 |
| C | 0 1 |
| 1 |
| 2 |
| C | 1 2 |
| 1 |
| 2 |
| C | 1 1 |
| 1 |
| 2 |
| C | 1 2 |
| C | 0 1 |
| 1 |
| 2 |
| C | 2 2 |
| 1 |
| 2 |
| C | 1 1 |
| 1 |
| 2 |
| C | 2 2 |
| a2 |
| 2 |

| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
| 4a+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1-2a |
| 2 |
| 1 |
| 2 |
| 1-2a2 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
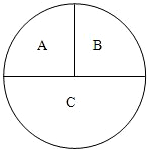 如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.
如图,一圆形靶分成A,B,C三部分,其面积之比为1:1:2.某同学向该靶投掷3枚飞镖,每次1枚.假设他每次投掷必定会中靶,且投中靶内各点是随机的.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分10分)
投掷A,B,C三个纪念币,正面向上的概率如下表所示![]() .
.
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
| 纪念币 | A | B | C |
| 概 率 |
| a | a |
将这三个纪念币同时投掷一次, 设![]() 表示出现正面向上的个数.
表示出现正面向上的个数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (i=0,1,2,3)中, 若
(i=0,1,2,3)中, 若![]() 的值最大, 求a的取值范围.
的值最大, 求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省苏北九所重点高中联考高三(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2009-2010学年江苏省南通市四星级高中高三(下)月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com