
【题目】已知函数![]()
(1)若![]() 为曲线
为曲线![]() 的一条切线,求a的值;
的一条切线,求a的值;
(2)已知![]() ,若存在唯一的整数
,若存在唯一的整数![]() ,使得
,使得![]() ,求a的取值范围.
,求a的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥C的底面是正方形,PA⊥平面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PEC
(2)求证:平面PCD⊥平面PEC;
(3)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科研人员在对人体脂肪含量和年龄之间关系的研究中,获得了一些年龄和脂肪含量的简单随机样本数据,如下表:

根据上表的数据得到如下的散点图.
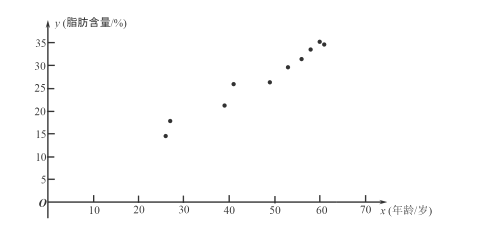
(1)根据上表中的样本数据及其散点图:
(i)求![]() ;
;
(ii)计算样本相关系数(精确到0.01),并刻画它们的相关程度.
(2)若y关于x的线性回归方程为![]() ,求
,求![]() 的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
的值(精确到0.01),并根据回归方程估计年龄为50岁时人体的脂肪含量。
附:参考数据:
参考公式:相关系数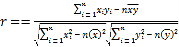
回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为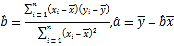
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.

现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 是长轴的一个端点,弦
是长轴的一个端点,弦![]() 过椭圆的中心O,点C在第一象限,且
过椭圆的中心O,点C在第一象限,且![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)设P、Q为椭圆上不重合的两点且异于A、B,若![]() 的平分线总是垂直于x轴,问是否存在实数
的平分线总是垂直于x轴,问是否存在实数![]() ,使得
,使得![]() ?若不存在,请说明理由;若存在,求
?若不存在,请说明理由;若存在,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:对任意两个正整数
满足:对任意两个正整数![]()
![]() ,
,![]() 与
与![]() 至少有一个成立,则称这个数列为“和谐数列”.
至少有一个成立,则称这个数列为“和谐数列”.
(Ⅰ)求证:若数列![]() 为等差数列,则
为等差数列,则![]() 为“和谐数列”;
为“和谐数列”;
(Ⅱ)求证:若数列![]() 为“和谐数列”,则数列
为“和谐数列”,则数列![]() 从第
从第![]() 项起为等差数列;
项起为等差数列;
(Ⅲ)若![]() 是各项均为整数的“和谐数列”,满足
是各项均为整数的“和谐数列”,满足![]() ,且存在
,且存在![]() 使得
使得![]() ,
,![]() ,求p的所有可能值.
,求p的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com