
【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣ax+a﹣1=0},C={x|x2﹣mx+2=0},且A∪B=A,A∩C=C,求实数a,m的取值范围.
【答案】解:由已知得A={1,2},B={x|(x﹣1)(x﹣a+1)=0},
由A∪B=A,知BA
因为B≠,当B为单元素集合时,只需a=2,此时B={1}满足题意.
当B为双元素集合时,只需a=3,此时B={1,2}也满足题意所以a=2或a=3,
由A∩C=C得CA
当C是空集时,△=m2﹣8<0即﹣2 ![]() <m<2
<m<2 ![]() ;
;
当C为单元素集合时,△=0,求得m=±2 ![]() ,此时C={
,此时C={ ![]() }或C={﹣
}或C={﹣ ![]() },此时不满足题意,舍去;
},此时不满足题意,舍去;
当C为双元素集合时,C只能为{1,2},此时m=3;
综上m的取值集合为{m|m=3或﹣2 ![]() <m<2
<m<2 ![]() }
}
【解析】本题考查的是集合的交、并集的运算。因为A∪B=A,知BA,当B≠时即B为单元素集合时,则a=2,此时B={1}满足题意.而当B为双元素集合时,则a=3,此时B={1,2}也满足题意所以a=2或a=3,又因为A∩C=C得CA,分情况讨论可得当C是空集时,△=m2﹣8<0即﹣2 ![]() <m<2
<m<2 ![]() ;
;
当C为单元素集合时,△=0,求得m=±2 ![]() ,此时C={
,此时C={ ![]() }或C={﹣
}或C={﹣ ![]() },此时不满足题意,舍去;当C为双元素集合时,C只能为{1,2},此时m=3;
},此时不满足题意,舍去;当C为双元素集合时,C只能为{1,2},此时m=3;
综上m的取值集合为{m|m=3或﹣2 ![]() <m<2
<m<2 ![]() }
}


科目:高中数学 来源: 题型:
【题目】某校举行“青少年禁毒”知识竞赛网上答题,高二年级共有500名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了100名学生的成绩进行统计.请你解答下列问题:
分组 | 频数 | 频率 |
[60,70) | 10 | 0.1 |
[70,80) | 22 | 0.22 |
[80,90) | a | 0.38 |
[90,100] | 30 | c |
合计 | 100 | d |

(1)根据下面的频率分布表和频率分布直方图,求出a+d和b+c的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中,其中正确的个数为( ) ①命题“若x2﹣3x+2=0,则x=1”的逆否命题为“若x≠1,则x2﹣3x+2=0”;
②“ ![]() ”是“cos2α=0”的充分不必要条件;
”是“cos2α=0”的充分不必要条件;
③若命题 ![]() ,则p:x∈R,x2+x+1=0;
,则p:x∈R,x2+x+1=0;
④若p∧q为假,p∨q为真,则p,q有且仅有一个是真命题.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n和为Sn , 且 ![]() 是
是 ![]() 与(an+1)2的等比中项.
与(an+1)2的等比中项.
(1)求证:数列{an}是等差数列;
(2)若 ![]() ,数列{bn}的前n项和为Tn , 求Tn .
,数列{bn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为4,P为BC的中点,Q为线段CC1上的动点(异于C点),过点A,P,Q的平面截面记为M.
则当CQ∈时(用区间或集合表示),M为四边形;
当CQ=时(用数值表示),M为等腰梯形;
当CQ=4时,M的面积为 . 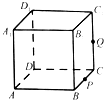
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0
(1)当方程C表示圆时,求m的取值范围;
(2)若圆C与直线l1:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(3)在(2)条件下,若圆C上存在四点到直线l2:x﹣2y+b=0的距离均为 ![]() ,试求b的取值范围.
,试求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,A={x| ![]() ≤2x≤8},B={x|x>0},C={x|m<x<m+2}
≤2x≤8},B={x|x>0},C={x|m<x<m+2}
(Ⅰ)求A∩(UB);
(Ⅱ)若A∩C=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱A1B1C1﹣A2B2C2中,各侧棱均垂直于底面,∠A1B1C1=90°,A1B1=B1C1=3,C1M=2B1N=2,则直线B1C1与平面A1MN所成角的正弦值为 . 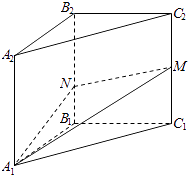
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H,则以下命题中,错误的命题是( ) 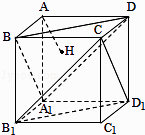
A.点H是△A1BD的垂心
B.AH垂直平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com