
【题目】已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0
(1)当方程C表示圆时,求m的取值范围;
(2)若圆C与直线l1:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(3)在(2)条件下,若圆C上存在四点到直线l2:x﹣2y+b=0的距离均为 ![]() ,试求b的取值范围.
,试求b的取值范围.
【答案】
(1)解:由方程C:x2+y2﹣2x﹣4y+m=0变为(x﹣1)2+(y﹣2)2=5﹣m
当5﹣m>0即m<5时,方程C表示圆;
(2)解:圆心(1,2)到直线l的距离d= ![]() =
= ![]() ,
,
∵弦长|MN|= ![]() ,
,
∴( ![]() )2+(
)2+( ![]() )2=5﹣m,解得m=3.
)2=5﹣m,解得m=3.
故m=3.
(3)解:圆心(1,2)到直线l的距离d= ![]() ,
,
假设存在直线l:x﹣2y+b=0,使得圆上有四点到直线l的距离为 ![]() ,
,
必须 ![]() <|
<| ![]() ﹣
﹣ ![]() |,解得4﹣
|,解得4﹣ ![]() <b<2+
<b<2+ ![]()
【解析】(1)由方程C:x2+y2﹣2x﹣4y+m=0变为(x﹣1)2+(y﹣2)2=5﹣m.当5﹣m>0表示圆,解出即可.(2)利用点到直线的距离可得:圆心(1,2)到直线l的距离d,利用( ![]() )2+(
)2+( ![]() )2=5﹣m,即可解得m.(3)如图所示,圆心(1,2)到直线l的距离d=
)2=5﹣m,即可解得m.(3)如图所示,圆心(1,2)到直线l的距离d= ![]() ,假设存在直线l:x﹣2y+b=0,使得圆上有四点到直线l的距离为
,假设存在直线l:x﹣2y+b=0,使得圆上有四点到直线l的距离为 ![]() ,必须
,必须 ![]() <|
<| ![]() ﹣
﹣ ![]() |,解出即可.
|,解出即可.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣4=0与直线x﹣2y+1=0交于点p.
(1)求过点p且垂直于直线3x+4y﹣15=0的直线l1的方程;(结果写成直线方程的一般式)
(2)求过点P并且在两坐标轴上截距相等的直线l2方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣ax+a﹣1=0},C={x|x2﹣mx+2=0},且A∪B=A,A∩C=C,求实数a,m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进价是每件10元,根据一周的销售数据得出周销量P(件)与单价x(元)之间的关系如图折线所示,该网店与这种商品有关的周开支均为25元.
(I)根据周销量图写出周销量P(件)与单价x(元)之间的函数关系式;
(Ⅱ)写出周利润y(元)与单价x(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.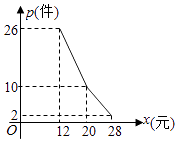
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对数函数f(x)=logax(a>0,且a≠1)的图象经过点(4,2).
(1)求实数a的值;
(2)如果f(x+1)<0,求实数x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com