
如图甲,⊙O的直径AB=2,圆上两点C、D在直径AB的两侧,且∠CAB= ,∠DAB=
,∠DAB= .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:

(1)求三棱锥C-BOD的体积;
(2)求证:CB⊥DE;
(3)在 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
(1)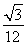 (2)见解析(3)G为
(2)见解析(3)G为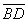 的中点
的中点
【解析】(1)∵C为圆周上一点,且AB为直径,∴∠C=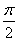 ,
,
∵∠CAB=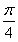 ,∴AC=BC,
,∴AC=BC,
∵O为AB的中点,∴CO⊥AB,
∵AB=2,∴CO=1.
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴CO⊥平面ABD,∴CO⊥平面BOD.
∴CO就是点C到平面BOD的距离,
S△BOD=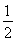 S△ABD=
S△ABD=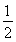 ×
×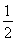 ×1×
×1×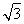 =
=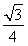 ,
,
∴VC-BOD=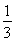 S△BOD·CO=
S△BOD·CO=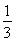 ×
×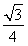 ×1=
×1=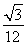 .
.
(2)证明:在△AOD中,∵∠OAD=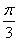 ,OA=OD,
,OA=OD,
∴△AOD为正三角形,
又∵E为OA的中点,∴DE⊥AO,
∵两个半圆所在平面ACB与平面ADB互相垂直且其交线为AB,
∴DE⊥平面ABC.
又CB?平面ABC,∴CB⊥DE.
(3)存在满足题意的点G,G为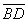 的中点.证明如下:
的中点.证明如下:
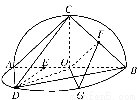
连接OG,OF,FG,
易知OG⊥BD,
∵AB为⊙O的直径,
∴AD⊥BD,
∴OG∥AD,
∵OG?平面ACD,AD?平面ACD,
∴OG∥平面ACD.
在△ABC中,O,F分别为AB,BC的中点,
∴OF∥AC,
∴OF∥平面ACD,
∵OG∩OF=O,
∴平面OFG∥平面ACD.
又FG?平面OFG,∴FG∥平面ACD.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练2练习卷(解析版) 题型:选择题
 6的展开式中x2的系数为( )
6的展开式中x2的系数为( )
A.-240 B.240
C.-60 D.60
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第1课时练习卷(解析版) 题型:选择题
对一批产品的长度(单位:毫米)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上为一等品,在区间[15,20)和[25,30)上为二等品,在区间[10,15)和[30,35]上为三等品.用频率估计概率,现从该批产品中随机抽取1件,则其为二等品的概率是( )

A.0.09 B.0.20 C.0.25 D.0.45
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:解答题
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.

(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:选择题
已知圆C1:(x-2)2+(y-3)2=1,圆C2:(x-3)2+(y-4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
A.5 -4 B.
-4 B. -1
-1
C.6-2 D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:解答题
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.

求证:(1)平面EFG∥平面ABC;(2)BC⊥SA.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第2课时练习卷(解析版) 题型:选择题
设α,β是两个不同的平面,l是一条直线,以下命题正确的是( )
A.若l⊥α,α⊥β,则l?β B.若l∥α,α∥β,则l?β
C.若l⊥α,α∥β,则l⊥β D.若l∥α,α⊥β,则l⊥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第3课时练习卷(解析版) 题型:解答题
已知正项数列{an},其前n项和Sn满足6Sn= +3an+2,且a1,a2,a6是等比数列{bn}的前三项.
+3an+2,且a1,a2,a6是等比数列{bn}的前三项.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=a1bn+a2bn-1+…+anb1,n∈N*,证明:3Tn+1=2bn+1-an+1(n∈N*).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
在△ABC中,若∠A=120°, =-1,则|
=-1,则| |的最小值是( )
|的最小值是( )
A. B.2 C.
B.2 C. D.6
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com