
如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4.设圆C的半径为1,圆心在l上.

(1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
(1)y=3或3x+4y-12=0.(2)
【解析】(1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2),于是切线的斜率必存在.设过A(0,3)的圆C的切线方程为y=kx+3.
由题意,得 =1,解得k=0或k=-
=1,解得k=0或k=-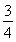 ,
,
故所求切线方程为y=3或3x+4y-12=0.
(2)因为圆心在直线y=2x-4上,所以圆C的方程为(x-a)2+[y-2(a-2)]2=1.
设点M(x,y),因为MA=2MO,
所以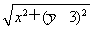 =2
=2 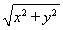 ,化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.
,化简得x2+y2+2y-3=0,即x2+(y+1)2=4,所以点M在以D(0,-1)为圆心,2为半径的圆上.
由题意,点M(x, y)在圆C上,所以圆C与圆D有公共点,
则|2-1|≤|CD|≤2+1,即1≤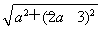 ≤3.
≤3.
整理,得-8≤5a2-12a≤0.由5a2-12a+8≥0,得a∈R;
由5a2-12a≤0,得0≤a≤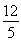 .所以点C的横坐标a的取值范围为
.所以点C的横坐标a的取值范围为


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练3练习卷(解析版) 题型:选择题
在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
A.32 B.0.2
C.40 D.0.25
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题6第2课时练习卷(解析版) 题型:选择题
1号箱中有2个白球和4个红球,2号箱中有5个白球和3个红球,现随机地从1号箱中取出一球放入2号箱,然后从2号箱随机取出一球,则从2号箱取出红球的概率是( )
A. B.
B. C.
C. D.
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:解答题
已知椭圆C的中心在坐标原点,焦点在x轴上且过点P ,离心率是
,离心率是 .
.
(1)求椭圆C的标准方程;
(2)直线l过点E (-1,0)且与椭圆C交于A,B两点,若|EA|=2|EB|,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第2课时练习卷(解析版) 题型:选择题
将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则( )
A.n=0 B.n=1 C.n=2 D.n≥3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题5第1课时练习卷(解析版) 题型:填空题
已知圆C:x2+y2-6x+8=0,则圆心C的坐标为________;若直线y=kx与圆C相切,且切点在第四象限,则k=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第3课时练习卷(解析版) 题型:解答题
如图甲,⊙O的直径AB=2,圆上两点C、D在直径AB的两侧,且∠CAB= ,∠DAB=
,∠DAB= .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:

(1)求三棱锥C-BOD的体积;
(2)求证:CB⊥DE;
(3)在 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题4第1课时练习卷(解析版) 题型:解答题
已知四棱锥P-ABCD的正视图是一个底边长为4、腰长为3的等腰三角形,如图分别是四棱锥P-ABCD的侧视图和俯视图.

(1)求证:AD⊥PC;
(2)求四棱锥P-ABCD的侧面PAB的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第4课时练习卷(解析版) 题型:解答题
已知函数f(x)=2sin xcos x+2 cos2x-
cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最小正周期;
(2)在锐角△ABC中,若f(A)=1, ·
· =
= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com