
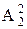 种方法; ⅱ) 学生再坐其余位置,有
种方法; ⅱ) 学生再坐其余位置,有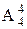 种方法.
种方法. 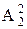 ·
·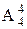 =48种坐法.
=48种坐法. 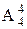 ; ⅱ) 教师坐中间位置:
; ⅱ) 教师坐中间位置: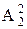 .
.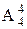 种坐法; ⅱ) 教师插入中间:
种坐法; ⅱ) 教师插入中间: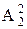 .
.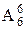 种坐法; ⅱ) 两位教师都不坐中间:
种坐法; ⅱ) 两位教师都不坐中间: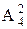 (先固定法)·
(先固定法)·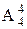 ;
;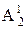 (甲坐中间) ·
(甲坐中间) ·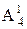 (再固定乙不坐中间) ·
(再固定乙不坐中间) ·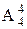 · 2(甲、乙互换);
· 2(甲、乙互换);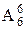 -(
-(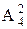
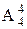 +2
+2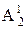
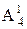
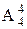 )
)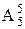 种坐法,而每个人坐中间位置的机会是均等的,应占所有坐法的1/5,即教师1人坐
种坐法,而每个人坐中间位置的机会是均等的,应占所有坐法的1/5,即教师1人坐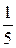
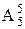
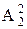 即
即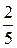
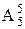 种。
种。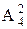 ;其他人再坐余下的3个位置:
;其他人再坐余下的3个位置: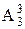 ;教师内部又有
;教师内部又有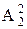 种坐法. ∴ 共有
种坐法. ∴ 共有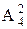
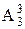
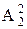 =144种坐法.
=144种坐法.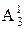
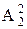 ;再排学生:
;再排学生: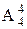 . ∴ 共有
. ∴ 共有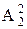
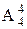
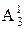 种坐法。
种坐法。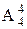
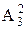 (教师插空).
(教师插空). 

科目:高中数学 来源:不详 题型:单选题
| A.8种 | B.9种 | C.10种 | D.11种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
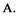 180对 B.21对 C.121对 D.60对
180对 B.21对 C.121对 D.60对查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A. 1344种 | B. 1248种 | C. 1056种 | D. 960种 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.9 | B.11 | C.13 | D.15 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
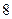 人,从男生中选
人,从男生中选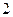 人,从女生中选
人,从女生中选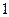 人分别参加数学、
人分别参加数学、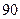 种不同方案,那么男、女生人数分别是( ).
种不同方案,那么男、女生人数分别是( ).A.男生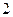 人,女生 人,女生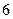 人 人 | B.男生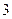 人,女生 人,女生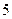 人 人 |
C.男生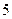 人,女生 人,女生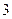 人 人 | D.男生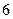 人,女生 人,女生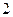 人 人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com