
【题目】已知函数![]() ,
,![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() .记
.记![]() .给出下列关于函数
.给出下列关于函数![]() 的说法:①当
的说法:①当![]() 时,
时,![]() ;②函数
;②函数![]() 为奇函数;③函数
为奇函数;③函数![]() 在
在![]() 上为增函数;④函数
上为增函数;④函数![]() 的最小值为
的最小值为![]() ,无最大值.其中正确的是______.
,无最大值.其中正确的是______.
【答案】①③
【解析】
g(x) ,F(x)=max{f(x),g(x)}(x∈R)
,F(x)=max{f(x),g(x)}(x∈R) .画出图象,数形结合即可得出.
.画出图象,数形结合即可得出.
由![]() 为偶函数,且当
为偶函数,且当![]() 时,
时,![]() ,
,
∴令![]() ,则
,则![]() ,则
,则![]() ,
,
即当![]() 时,
时,![]() ,
,
∴g(x) ,
,
F(x)=max{f(x),g(x)}(x∈R) .
.
画出图象,
由图象可得:①当x≥6时,∵x2﹣4x≥2x,∴F(x)=x2﹣4x,因此正确.
②由图象可得:函数F(x)不为奇函数,因此不正确.
③﹣2≤x≤6时,2x>x2﹣4x,可得函数F(x)=2x,因此函数F(x)在[﹣2,6]上为增函数,所以函数F(x)在[﹣2,2]上为增函数是正确的.
④x≤﹣2时,g(x)=x2+4x≥2x,可得F(x)=x2+4x≥﹣4,综合可得函数F(x)的最小值为﹣4,无最大值,④不正确.
其中正确的是 ①③.
故答案为①③.


科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
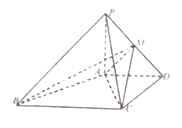
(1)求证:![]() ;
;
(2)在线段![]() 上,是否存在一点
上,是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,如果存在,求
,如果存在,求![]() 与平面
与平面![]() 所成角的正弦值,如果不存在,请说明理由.
所成角的正弦值,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.
(Ⅰ)求抛物线方程;
(Ⅱ)点P为准线上任意一点,AB为抛物线上过焦点的任意一条弦,设直线PA,PB,PF的斜率为k1,k2,k3,问是否存在实数λ,使得k1+k2=λk3恒成立.若存在,请求出λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有20种不同的零食,每100g可食部分包含的能量(单位:kJ)如下:
110 120 123 165 432 190 174 235 428 318
249 280 162 146 210 120 123 120 150 140
(1)以上述20个数据组成总体,求总体平均数与总体标准差
(2)设计恰当的随机抽样方法,从总体中抽取一个容量为7的样本.
(3)利用上面的抽样方法,再抽取容量为7的样本,这个样本的平均数和标准差与(2)中的结果一样吗?为什么?
(4)利用(2)中的随机抽样方法,分别从总体中抽取一个容量为10,13,16,19的样本,分析样本容量与样本的平均数和标准差对总体的估计效果之间有什么关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券.例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国民法总则》(以下简称《民法总则》)自2017年10月1日起施行。作为民法典的开篇之作,《民法总则》与每个人的一生息息相关.某地区为了调研本地区人们对该法律的了解情况,随机抽取50人,他们的年龄都在区间[25,85]上,年龄的频率分布及了解《民法总则》的人数如下表:
年龄 | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) | [75,85) |
频数 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法总则》 | 1 | 2 | 8 | 12 | 4 | 5 |
(Ⅰ)填写下面2×2 列联表,并判断是否有99%的把握认为以45岁为分界点对了解《民法总则》政策有差异;

(Ⅱ)若对年龄在[45,55),[65,75)的被调研人中各随机选取2人进行深入调研,记选中的4人中不了解《民法总则》的人数为X,求随机变量X的分布列和数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为1的动圆与定圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是( )
A. (x-5)2+(y+7)2=25
B. (x-5)2+(y+7)2=3或(x-5)2+(y+7)2=15
C. (x-5)2+(y+7)2=9
D. (x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为 (参考数据:![]() ,
,![]() ,
,![]() )
)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com