
 名工人的日加工零件数(单位:件),获得数据如下:
名工人的日加工零件数(单位:件),获得数据如下: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,根据上述数据得到样本的频率分布表如下:
,根据上述数据得到样本的频率分布表如下:| 分组 | 频数 | 频率 |
 |  |  |
 |  | 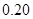 |
 | 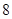 | 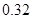 |
 |  |  |
 |  | 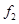 |
 、
、 、
、 和
和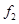 的值;
的值; 人,至少有
人,至少有 人的日加工零件数落在区间
人的日加工零件数落在区间 的概率.
的概率.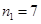 ,
,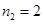 ,
,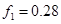 ,
,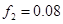 ;(2)详见解析;(3)
;(2)详见解析;(3)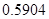 .
. 、
、 、
、 和
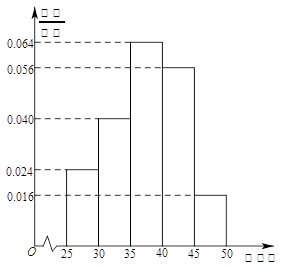
和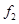 的值;(2)根据频率分布表中的信息求出各组的
的值;(2)根据频率分布表中的信息求出各组的 的值,以此为相应组的纵坐标画出频率分布直方图;(3)先确定所取的
的值,以此为相应组的纵坐标画出频率分布直方图;(3)先确定所取的 人中日加工零件数了落在区间
人中日加工零件数了落在区间 的人数所服从的相应的概率分布(二项分布),然后利用独立重复试验与对立事件求出题中事件的概率.
的人数所服从的相应的概率分布(二项分布),然后利用独立重复试验与对立事件求出题中事件的概率.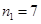 ,
,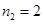 ,
,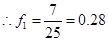 ,
,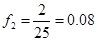 ;
;
 的概率
的概率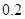 ,
, 人中,日加工零件数落在区间
人中,日加工零件数落在区间 的人数为
的人数为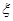 ,则
,则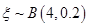 ,
,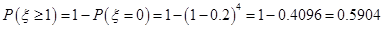 ,
, 人中,至少有
人中,至少有 人的日加工零件数落在区间
人的日加工零件数落在区间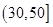 的概率约为
的概率约为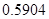 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
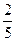 ,乙投进的概率为
,乙投进的概率为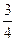 ,两人投进与否相互没有影响,现两人各投1次,求:
,两人投进与否相互没有影响,现两人各投1次,求:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 不得禽流感 | 得禽流感 | 总计 |
| 服药 | | | |
| 不服药 | | | |
| 总计 | | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
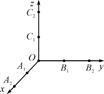
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 和
和 ,假设两人射击目标是否击中相互之间没有影响,每人各次射击是否击中目标也没有影响.则两人各射击4次,甲恰好有2次击中目标且乙恰好有3次击中目标的概率为________.
,假设两人射击目标是否击中相互之间没有影响,每人各次射击是否击中目标也没有影响.则两人各射击4次,甲恰好有2次击中目标且乙恰好有3次击中目标的概率为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个球,求
个球,求 的分布列及期望
的分布列及期望 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.36 | B.0.216 | C.0.432 | D.0.648 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com