
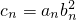 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn; -------(1分)
-------(1分) ----(2分)
----(2分) ,bn=b1qn-1=
,bn=b1qn-1=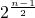 -------(4分)
-------(4分) -----------------①
-----------------① ---------------------------②
---------------------------② --------------------------(7分)
--------------------------(7分) --------------------------(9分)
--------------------------(9分) -------(10分),
-------(10分), -----(12分),
-----(12分), ,
, -------(13分)
-------(13分) )+
)+ =
= =
= ------(15分)
------(15分) ,
, 时,an=p+log2(Tn+c)恒成立-------(16分)
时,an=p+log2(Tn+c)恒成立-------(16分) ,由b3=b1q2且q>0得q=
,由b3=b1q2且q>0得q= ,从而可求an,bn;
,从而可求an,bn; ,令n=1,n=3,求得c=
,令n=1,n=3,求得c= ,
, ,再验证下即可.
,再验证下即可.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
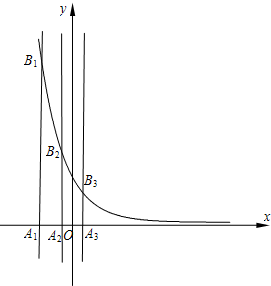 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=(| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省泰州市靖江市高三(上)期中数学试卷(解析版) 题型:解答题
 ,求数列{cn}的前n项和Sn;
,求数列{cn}的前n项和Sn;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com