
 =a,
=a, =b,
=b, =с,
=с, =d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?
=d,且a·b=b·с=с·d=d·a,试问四边形ABCD是什么图形?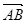 ,
, ,
, ,
, 是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;(2)由已知条件产生数量积的关键是构造数量积,因为数量积的定义式中含有边、角两种关系。
是顺次首尾相接向量,则其和向量是零向量,即a+b+с+d=0,应注意这一隐含条件应用;(2)由已知条件产生数量积的关键是构造数量积,因为数量积的定义式中含有边、角两种关系。

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:单选题
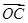 =
=
 +
+
 ,其中
,其中 ,
, ∈R,
∈R, +
+ =1,则点C的轨迹为
=1,则点C的轨迹为| A.平面 | B.直线 | C.圆 | D.线段 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com