
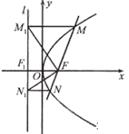
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1

(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅰ) 略(Ⅱ)成立。
本小题主要考查抛物线的概念,抛物线的几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力(满分13分)
(1) 证法1:由抛物线的定义得
![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() 2分
2分
如图,设准线l与x的交点为![]()
![]()
![]()
而![]()
即![]()
![]()
故![]()
证法2:依题意,焦点为![]() 准线l的方程为
准线l的方程为![]()
设点M,N的坐标分别为![]() 直线MN的方程为
直线MN的方程为![]() ,则有
,则有
![]()
由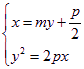 得
得![]()
于是,![]() ,
,![]()
![]() ,故
,故![]()
(Ⅱ)![]() 成立,证明如下:
成立,证明如下:
证法1:设![]() ,则由抛物线的定义得
,则由抛物线的定义得
![]() ,于是
,于是
![]()
![]()
![]()
![]()
![]()
将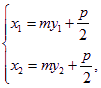 与
与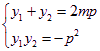 代入上式化简可得w.w.w.k.s.5.u.c.o.m
代入上式化简可得w.w.w.k.s.5.u.c.o.m ![]()
![]()
![]() ,此式恒成立。
,此式恒成立。
故![]() 成立。
成立。
证法2:如图,设直线![]() M的倾角为
M的倾角为![]() ,
,![]()
则由抛物线的定义得![]()
![]()
于是![]()
在![]() 和
和![]() 中,由余弦定理可得
中,由余弦定理可得
![]()
由(I)的结论,得![]()
![]()
即![]() ,得证。
,得证。


科目:高中数学 来源: 题型:
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1

(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为![]() ,试判断S22=4S1S3是否成立,并证明你的结论。w.w.w.k.s.5.u.c.o.m
,试判断S22=4S1S3是否成立,并证明你的结论。w.w.w.k.s.5.u.c.o.m ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1
 (Ⅰ)求证:FM1⊥FN1:
(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。 ![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省镇平一高高三下学期第四次周考文科数学试卷 题型:选择题
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
A.y2=9x B.y2=6x
C.y2=3x D.y2= x
x
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校联考高二下学期期中考试数学(理) 题型:选择题
如图,过抛物线y2=2px(p>0)的焦点F的直线 交抛物线
交抛物线
于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,
则此抛物线的方程为 ( )

A.y2=3x B.y2=6x C.y2=9x D.y2=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com