
分析 画出函数f(x)=$\left\{\begin{array}{l}|{lnx}|,({0<x≤{e^2}})\\{e^2}+2-x,({x>{e^2}})\end{array}$的图象,可得$\frac{f({x}_{3})}{{x}_{1}{{x}_{2}}^{2}}$=$\frac{{lnx}_{2}}{{x}_{2}}$,(x2∈(1,e2)),利用导数法,可得其最大值.
解答 解:画出函数f(x)=$\left\{\begin{array}{l}|{lnx}|,({0<x≤{e^2}})\\{e^2}+2-x,({x>{e^2}})\end{array}$的图象如下图所示:
若存在x1<x2<x3,使f(x1)=f(x2)=f(x3),
则x1•x2=1,f(x2)=f(x3)=lnx2,
∴$\frac{f({x}_{3})}{{x}_{1}{{x}_{2}}^{2}}$=$\frac{{lnx}_{2}}{{x}_{2}}$,(x2∈(1,e2)),
令y=$\frac{lnx}{x}$,x∈(1,e2),
则y′=$\frac{1-lnx}{{x}^{2}}$,
∴x∈(1,e),y′>0,x∈(e,e3),y′<0,
∴函数在(1,e)上单调递增,在(e,e3)上单调递减,
∴x=e时,函数取得最大值$\frac{1}{e}$,
∴$\frac{f({x}_{3})}{{x}_{1}{{x}_{2}}^{2}}$的最大值为$\frac{1}{e}$.
故答案为:$\frac{1}{e}$
点评 本题考查分段函数的应用,考查利用导数求最值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
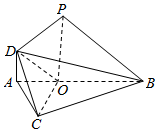 如图,∠ABC=$\frac{π}{4}$,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
如图,∠ABC=$\frac{π}{4}$,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 001,041,…761 | B. | 031,071,…791 | C. | 027,067,…787 | D. | 055,095,…795 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
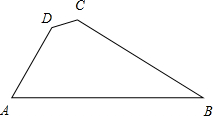 如图,四边形ABCD中,若∠DAB=60°,∠ABC=30°,∠BCD=120°,AD=2,AB=5.
如图,四边形ABCD中,若∠DAB=60°,∠ABC=30°,∠BCD=120°,AD=2,AB=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com