
(2)把sin![]() 、cos
、cos![]() 转化成cosα、sinα的表达式,则tan
转化成cosα、sinα的表达式,则tan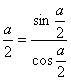 = ___________= ________.
= ___________= ________.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省嘉兴市高三上学期基础测试文科数学试卷(解析版) 题型:选择题
若把函数y=f(x)的图像沿x轴向左平移 个单位,沿y轴向下平移1个单位,然后再把图像上每个点的橫坐标伸长到原来的2位(纵坐标保持不变),得到函数y=cosx的图像,则y=f(x)的解析式为:
个单位,沿y轴向下平移1个单位,然后再把图像上每个点的橫坐标伸长到原来的2位(纵坐标保持不变),得到函数y=cosx的图像,则y=f(x)的解析式为:
A.y=cos(2x- )+1 B.
)+1 B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com