
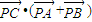 的最小值是 .
的最小值是 . 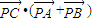 =2(x-
=2(x- )2+2(y-
)2+2(y- )2-1,结合两点间的距离公式可得点P坐标为(
)2-1,结合两点间的距离公式可得点P坐标为( ,
, )时,
)时,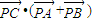 取得最小值.
取得最小值.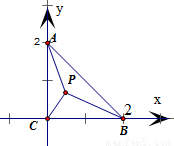
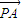 =(-x,2-y),
=(-x,2-y),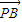 =(2-x,-y)),
=(2-x,-y)),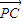 =(-x,-y)
=(-x,-y)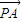 +
+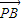 =(2-2x,2-2y)
=(2-2x,2-2y)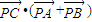 =-x(2-2x)-y(2-2y)=-2x+2x2-2y+2y2=2(x-
=-x(2-2x)-y(2-2y)=-2x+2x2-2y+2y2=2(x- )2+2(y-
)2+2(y- )2-1
)2-1 )2+(y-
)2+(y- )2为点P到点(
)2为点P到点( ,
, )距离的平方,
)距离的平方, ,
, )时,(x-
)时,(x- )2+(y-
)2+(y- )2达到最小值0,
)2达到最小值0, ,
, )时,数量积
)时,数量积 的最小值是-1
的最小值是-1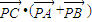 的最小值.着重考查了平面向量数量积的坐标表示及其应用,属于中档题.解题的关键是根据所求式子运用几何意义使问题得以解决.
的最小值.着重考查了平面向量数量积的坐标表示及其应用,属于中档题.解题的关键是根据所求式子运用几何意义使问题得以解决. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
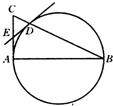 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com