分析:先根据圆C
1的方程找出圆心坐标与半径R的值,找出圆C
2的半径的最大时的情况:当圆c
2的圆心Q为线段AB的中点时,圆c
2与圆C
1相切,切点在圆C
1的劣弧
上,设切点为P,此时圆C
2的半径r的最大.求r的方法是,联立直线与圆的方程,消去y后得到关于x的一元二次方程,利用韦达定理求出Q的横坐标,把Q的横坐标代入直线方程即可求出Q的纵坐标,得到Q的坐标,利用两点间的距离公式求出两圆心的距离OQ等于d,然后根据两圆内切时,两圆心之间的距离等于两半径相减可得圆C
2的半径最大值.
解答: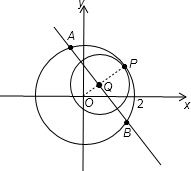
解:由圆C
1:x
2+y
2=4,可得圆心O(0,0),半径R=2
如图,当圆c
2的圆心Q为线段AB的中点时,圆c
2与圆C
1相切,切点在圆C
1的劣弧
上,设切点为P,此时圆C
2的半径r的最大.
联立直线与圆的方程得
,消去y得到25x
2-30x-39=0,
设A(x
1,y
1),B(x
2,y
2),则x
1+x
2=
,所以线段AB的中点Q的横坐标为
,把x=
代入直线方程中解得y=
,
所以Q(
,
),则两圆心之间的距离OQ=d=
=1,
因为两圆内切,所以圆c
2的最大半径r=R-d=2-1=1
故答案为:1
点评:此题考查学生掌握两圆内切时两半径所满足的条件,灵活运用韦达定理及两点间的距离公式化简求值,是一道中档题.



 解:由圆C1:x2+y2=4,可得圆心O(0,0),半径R=2
解:由圆C1:x2+y2=4,可得圆心O(0,0),半径R=2




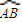 上,则圆C2的半径的最大值是 .
上,则圆C2的半径的最大值是 .