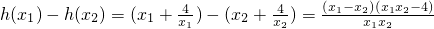已知f(x)=lgx:
(1)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式,如从f(x)=lgx可抽象出性质:f(x1•x2)=f(x1)+f(x2).
对于下面两个具体函数,试分别抽象出一个与上面类似的性质:
由h(x)=2x可抽象出性质为______,
由φ(x)=3x+1可抽象出性质为______.
(2)g(x)=f(x2+6x+4)-f(x),求g(x)的最小值.
解:(1)h(x)满足h(x
1+x
2)=h(x
1)•h(x
2)
φ(x)满足φ(x
1+x
2)=φ(x
1)+φ(x
2)
故答案为:h(x
1+x
2)=h(x
1)•h(x
2),φ(x
1+x
2)=φ(x
1)+φ(x
2)(答案不唯一)
(2)g(x)=f(x
2+6x+4)-f(x)=lg(x
2+6x+4)-lgx
=

令
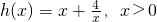
,
任取0<x
1<x
2,
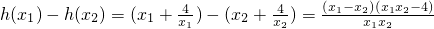
当0<x
1<x
2≤2时,h(x
1)-h(x
2)>0,h(x
1)>h(x
2),
当2≤x
1<x
2时,h(x
1)-h(x
2)<0,h(x
1)<h(x
2),
h(x)在(0,2]上单调递减,在[2,+∞)上单调递增,
故当x=2时,h
min(x)=4,这时g
min(x)=1.
分析:(1)根据对数函数的性质可得h(x)满足h(x
1+x
2)=h(x
1)•h(x
2),根据一次函数的性质可得φ(x)满足φ(x
1+x
2)=φ(x
1)+φ(x
2)
(2)由已知中f(x
1•x
2)=f(x
1)+f(x
2),求出函数g(x)的解析式,并分析函数的单调性,进而可得函数的最值.
点评:本题考查的知识点是抽象函数及其应用,函数单调性的判断与证明,其中(1)的结论是解答抽象函数时,将“抽象”化为“具体”的常用结论,请注意总结.


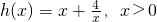 ,
,