已知数列{an}满足:a1=1,a2=a(a>0),数列{bn}满足bn=anan+1(n∈N*)
(Ⅰ)若{an}是等差数列,且b3=12,求数列{an}的通项公式.
(Ⅱ)若{an}是等比数列,求数列{bn}的前n项和Sn.
(Ⅲ)若{bn}是公比为a-1的等比数列时,{an}能否为等比数列?若能,求出a的值;若不能,请说明理由.
【答案】
分析:(Ⅰ)在b
n表达式中取n=3,结合等差数列的通项公式解出公差d,从而得出数列{a
n}的通项公式;
(Ⅱ)由等比数列的通项公式求出数列{a
n}的通项公式,再代入b
n=a
na
n+1 ,得出数列{b
n}的通项公式,最后用等比数列求和公式算出结果;
(Ⅲ)先假设命题正确,再利用数列{a
n}的前3项得出矛盾,从而说明,数列{a
n}不能为等比数列.
解答:解:(Ⅰ)∵{a
n}是等差数列a
1=1,a
2=a,b
n=a
na
n+1,b
3=12
∴b
3=a
3a
4=(a
1+2d)((a
1+3d)=(1+2d)(1+3d)=12
即d=1或d=
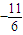
又因a=a
1+d=1+d>0得d>-1
∴d=1
∴a
n=n(4分)
(Ⅱ){a
n}是等比数列,首项a
1=1,a
2=a,故公比
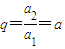
,
所以a
n=a
n-1,代入{b
n}的表达式得
b
n=a
na
n+1=a
2n-1,可得
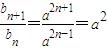
∴数列{b
n}是以a为首项,公比为 a
2的等比数列
故S
n=
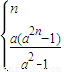
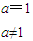
(5分)
(Ⅲ){a
n}不能为等比数列,理由如下:
∵b
n=a
na
n+1,{b
n}是公比为a-1的等比数列
∴
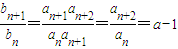
∴a
3=a-1
假设{a
n}为等比数列,由a
1=1,a
2=a得a
3=a
2,所以a
2=a-1
因此此方程无解,所以数列一定不能等比数列.(14分)
点评:抓住等差数列的首项和公差,等比数列的首项和公比是解决这类问题的关键,求等比数列的前n项和注意公比能不能等于1的分类讨论.

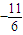
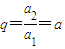 ,
,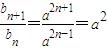
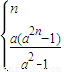
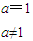 (5分)
(5分)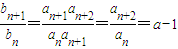


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案