
甲乙两人各自在300米长的直线形跑道上跑步,则在任一时刻两人在跑道上相距不超过50米的概率是多少( ).
A.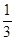 | B.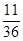 | C.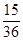 | D.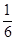 |
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:单选题
在长为12cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于36cm2与81cm2之间的概率为( )
A.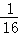 | B. | C.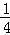 | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当
 3.841时,认为两个事件无关,当
3.841时,认为两个事件无关,当 >6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
>6.635时,有99%的把握说明两个事件有关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 =20.87,根据这一数据,认为打鼾与患心脏病之间( )
=20.87,根据这一数据,认为打鼾与患心脏病之间( )
| A.认为两者无关 | B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 | D.约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设集合A={2,4,6,8},B={1,3,5,7,9},今从A中取一个数作为十位数字,从B中取一个数作为个位数字,问:
(1)能组成多少个不同的两位数?
(2)能组成多少个十位数字小于个位数字的两位数?
(3)能组成多少个能被3整除的两位数?
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一数学兴趣小组利用几何概型的相关知识做试验计算圆周率,他们向一个边长为1米的正方形区域均匀撒豆,测得正方形区域有豆5120颗,正方形的内切圆区域有豆4009颗,则他们所测得的圆周率约为(保留三位有效数字)( )
| A.3.13 | B.3.14 | C.3.15 | D.3.16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com