
如图,在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,最大容积是 .
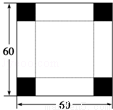
16000cm3.
【解析】
试题分析:设箱底边长为xcm,结合题意可得容积V(x)= (60x2﹣x3)(0<x<60).再用导数工具研究V(x)在区间(0,60)上的单调性,可知当x=40时V(x)达到最大值.由此得到本题答案.
(60x2﹣x3)(0<x<60).再用导数工具研究V(x)在区间(0,60)上的单调性,可知当x=40时V(x)达到最大值.由此得到本题答案.
【解析】
设箱底边长为xcm,则箱高h=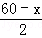 ,
,
∴箱子容积V(x)=x2h= (60x2﹣x3)(0<x<60).
(60x2﹣x3)(0<x<60).
求导数,得V′(x)=60x﹣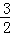 x2,
x2,
令V′(x)=60x﹣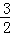 x2=0,解得x=0(不合题意,舍去),x=40,
x2=0,解得x=0(不合题意,舍去),x=40,
∵x∈(0,40)时,V′(x)>0;x∈(40,60)时,V′(x)<0
∴V(x)在区间(0,40)上为增函数,区间(40,60)上为减函数
由此可得V(x)的最大值是V(40)=16000.
故答案为:16000cm3.


科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
(2014•揭阳三模)如图,以AB=4为直径的圆与△ABC的两边分别交于E,F两点,∠ACB=60°,则EF= .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:选择题
若P=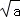 +
+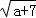 ,Q=
,Q=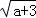 +
+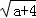 (a≥0),则P,Q的大小关系是( )
(a≥0),则P,Q的大小关系是( )
A.P>Q B.P=Q C.P<Q D.由a的取值确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:解答题
某种产品每件成本为6元,每件售价为x元(x>6),年销量为u万件,若已知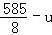 与
与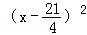 成正比,且售价为10元时,年销量为28万件.
成正比,且售价为10元时,年销量为28万件.
(1)求年销售利润y关于x的函数关系式.
(2)求售价为多少时,年利润最大,并求出最大年利润.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
某工厂要围建一个面积为512平方米的矩形堆料场,一边可以利用原有的墙壁,其它三边需要砌新的墙壁,当砌壁所用的材料最省时,堆料场的长和宽分别为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.2导数的运算练习卷(解析版) 题型:解答题
求下列函数的导数:
(1)y=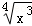 +2x;
+2x;
(2)y=lgx﹣sinx;
(3)y=2sinxcosx;
(4)y=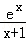 .
.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:解答题
直线l过点M(1,1),与椭圆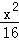 +
+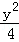 =1交于P,Q两点,已知线段PQ的中点横坐标为
=1交于P,Q两点,已知线段PQ的中点横坐标为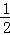 ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.1圆锥曲线练习卷(解析版) 题型:选择题
以坐标轴为对称轴,以原点为顶点且过圆x2+y2﹣2x+6y+9=0的圆心的抛物线的方程是( )
A.y=3x2或y=﹣3x2 B.y=3x2
C.y2=﹣9x或y=3x2 D.y=﹣3x2或y2=9x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com