已知{an}为递增的等比数列,且{a1,a3,a5}?{-10,-6,-2,0,1,3,4,16}.
(I)求数列{an}的通项公式;
(II)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
【答案】
分析:(I)由{a
n}为递增的等比数列,得到数列{a
n}的公比q>0,且a
1>0,又{a
1,a
3,a
5}?{-10,-6,-2,0,1,3,4,16},可得出a
1,a
3,a
5三项,则公比可求,通项可求.
(II)先假设存在等差数列{b
n},由所给式子求出b
1,b
2,公差可求,通项可求,证明当b
n=n时,a
1b
n+a
2b
n-1++a
n-1b
2+a
nb
1=2
n+1-n-2对一切n∈N*都成立,用错位相减法求得此数列是适合的.
解答:解:(I)因为{a
n}是递增的等比数列,所以数列{a
n}公比q>0,首项a
1>0,
又{a
1,a
3,a
5}?{-10,-6,-2,0,1,3,4,16},
所以a
1=1,a
3=4,a
s=16(3分)
从而
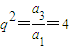
,q=2,a
n=a
1q
n-1=2
n-1所以数列{a
n}的通项公式为a
n=2
n-1(6分)
(II)假设存在满足条件的等整数列{b
n},其公差为d,则当n=1时,a
1b
1=1,
又∵a
1=1,∴b
1=1;
当n=2时,a
1b
2+a
2b
1=4,b
2+2b
1=4,b
2=2
则d=b
2-b
1=1,∴b
n=b
1+(n-1)d=1+(n-1)×1=n(8分)
以下证明当b
n=n时,a
1b
n+a
2b
n-1++a
n-1b
2+a
nb
1=2
n+1-n-2对一切n∈N*都成立.
设S
n=a
1b
n+a
2b
n-1+…+a
n-1b
2+a
nb
1,
即S
n=1×n+2×(n-1)+2
2×(n-2)+2
3×(n-3)+…+2
n-2×2+2
n-1×1,(1)
2S
n=2×n+2
2×(n-1)+2
3×(n-2)+…+2
n-1×2+2
n×1,(2)
(2)-(1)得S
n=-n+2+2
2+2
3++2
n-1+2
n=
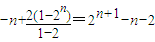
,
所以存在等差数列{b
n},b
n=n使得a
1b
n+a
2b
n-1+a
3b
n-2+a
nb
1=2
n+1-n-2对一切n∈N*都成立(12分)
点评:本小题主要考查等差数列、等比数列等基础知识,已知数列为等比数列,求通项公式,求首项和公比即可;用错位相减法求数列的前n项和,用时要观察项的特征,是否是等差数列的项与等比数列的项的乘积;考查推理论证能力、运算求解能力,考查特殊与一般思想.

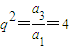 ,q=2,an=a1qn-1=2n-1
,q=2,an=a1qn-1=2n-1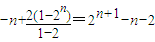 ,
,

 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.