Question

已知{a_n}为递增的等比数列，且{a₁，a₃，a₅}{－10，－6，－2,0,1,3,4,16}．

(1)求数列{a_n}的通项公式；

(2)是否存在等差数列{b_n}，使得a₁b_n＋a₂b_n－1＋a₃b_n－2＋…＋a_nb₁＝2ⁿ⁺¹－n－2对一切n∈N^*都成立？若存在，求出b_n；若不存在，说明理由．

 

Answer 1

【答案】

(1) a_n＝2^n－1，         (2) b_n＝n，

【解析】（1）由等比数列递增的性质得其首项为1，公比为4，可得到通项公式；（2）先由数列的前两项满足等式，求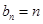出；再写出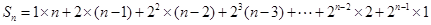,错位相减求出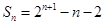。即证出存在数列{b_n}，结论成立

(1)因为{a_n}是递增的等比数列，所以数列{a_n}的公比是正数，

又{a₁，a₃，a₅}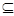{－10，－6，－2,0,1,3,4,16}，所以a₁＝1，a₃＝4，a₅＝16，

从而q²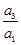＝＝4，q＝2，a_n＝a₁q^n－1＝2^n－1，所以数列{a_n}的通项公式为a_n＝2^n－1，

(2)假设存在满足条件的等差数列{b_n}，其公差为d.则当n＝1时，a₁b₁＝1，

又∵a₁＝1，∴b₁＝1；

当n＝2时，a₁b₂＋a₂b₁＝4，b₂＋2b₁＝4，b₂＝2.

则d＝b₂－b₁＝1，∴b_n＝b₁＋(n－1)d＝1＋(n－1)×1＝n.

以下证明当b_n＝n时，a₁b_n＋a₂b_n－1＋…＋a_n－1b₂＋a_nb₁＝2^n＋1－n－2对一切n∈N^*都成立．

设S_n＝a₁b_n＋a₂b_n－1＋…＋a_n－1b₂＋a_nb₁，

即S_n＝1×n＋2×(n－1)＋2²×(n－2)＋2³×(n－3)＋…＋2^n－2×2＋2^n－1×1，  ①

2S_n＝2×n＋2²×(n－1)＋2³×(n－2)＋…＋2^n－1×2＋2ⁿ×1，              ②

②－①得S_n＝－n＋2＋2²＋2³＋…＋2^n－1＋2ⁿ＝－n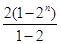＋＝2^n＋1－n－2，

所以存在等差数列{b_n}，b_n＝n，使得a₁b_n＋a₂b_n－1＋…＋a_n－1b₂＋a_nb₁＝2^n＋1－n－2对一切n∈N^*都成立.