分析:(Ⅰ)先根据△ABC为正三角形,D为AC中点,得到BD⊥AC,求出△BCD的面积;再根据C1C⊥底面ABC即可求出三棱锥C1-BCD的体积;
(Ⅱ)先根据A1A⊥底面ABC,得到A1A⊥BD,再结合BD⊥AC即可得到BD⊥平面ACC1A1.即可证:平面BC1D⊥平面ACC1A1;
(Ⅲ)连接B1C交BC1于O,连接OD,根据D为AC中点,O为B1C中点可得OD∥AB1,即可证:直线AB1∥平面BC1D.
解答: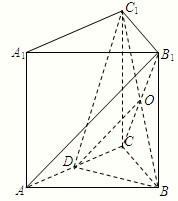
(本小题满分12分)
解:(Ⅰ)∵△ABC为正三角形,D为AC中点,
∴BD⊥AC,
由AB=6可知,
CD=3,BD=3,
∴
S△BCD=•CD•BD=.
又∵A
1A⊥底面ABC,且A
1A=AB=6,
∴C
1C⊥底面ABC,且C
1C=6,
∴
VC1-BCD=•S△BCD•C1C=9. …(4分)
(Ⅱ)∵A
1A⊥底面ABC,
∴A
1A⊥BD.
又BD⊥AC,
∴BD⊥平面ACC
1A
1.
又BD?平面BC
1D,
∴平面BC
1D⊥平面ACC
1A
1. …(8分)
(Ⅲ)连接B
1C交BC
1于O,连接OD,
在△B
1AC中,D为AC中点,O为B
1C中点,
所以OD∥AB
1,
又OD?平面BC
1D,
∴直线AB
1∥平面BC
1D. …(12分)
点评:本题主要考查平面与平面垂直的判定以及直线与平面平行的判定和棱锥体积的计算.在证明线面平行时,一般常用做法是证明面面平行或证明线线平行.

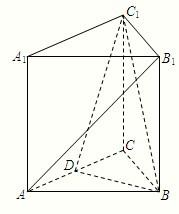 如图,三棱柱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,A1A=AB=6,D为AC中点.
如图,三棱柱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,A1A=AB=6,D为AC中点. (本小题满分12分)
(本小题满分12分)

 名校课堂系列答案
名校课堂系列答案 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=