(Ⅰ):证明:∵
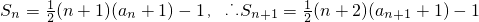
∴
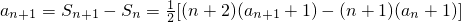
整理,得na
n+1=(n+1)a
n-1①
∴(n+1)a
n+2=(n+2)a
n+1-1②
②-①得:(n+1)a
n+2-na
n+1=(n+2)a
n+1-(n+1)a
n即(n+1)a
n+2-2(n+1)a
n+1+(n+1)a
n=0∴a
n+2-2a
n+1+a
n=0,
即a
n+2-a
n+1=a
n+1-a
n∴数列{a
n}是等差数列
(II)∵a
1=3,na
n+1=(n+1)a
n-1,
∴a
2=2a
1-1=5∴a
2-a
1=2,
即等差数列{a
n}的公差为2,
∴a
n=a
1+2(n-1)=2n+1,(n∈N
*)
分析:(I)知通项与前n项和的关系,通过仿写得到两个等式,作差据和与项的关系求出项的递推关系,据等差中项的方法得证.
(II)利用等差数列的通项公式求出通项.
点评:本题考查由项与和的递推关系求项的特定关系:通过仿写作差;等差数列的通项公式.

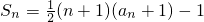
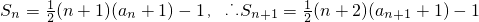
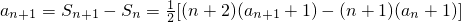


 名校课堂系列答案
名校课堂系列答案