
分析 利用复数代数形式的乘除运算化简复数z,然后代入ω=z+ai,再求出$\frac{ω}{z}$,由复数求模公式求出$|\frac{ω}{z}|$,求解一元二次不等式可得答案.
解答 解:$z=\frac{(-1+3i)(1-i)-(1+3i)}{i}=\frac{(2+4i)-(1+3i)}{i}=\frac{1+i}{i}=1-i$,
∵ω=z+ai=1-i+ai=1+(a-1)i,
∴$\frac{ω}{Z}=\frac{1+(a-1)i}{1-i}=\frac{[1+(a-1)i](1+i)}{2}=\frac{2-a+ai}{2}$.
∴$|\frac{ω}{z}|=\frac{{\sqrt{{{(2-a)}^2}+{a^2}}}}{2}≤\sqrt{2}$,
∴a2-2a-2≤0,
解得$1-\sqrt{3}≤a≤1+\sqrt{3}$.
故a的取值范围是[$1-\sqrt{3},1+\sqrt{3}$].
点评 本题考查了复数代数形式的混合运算,考查了复数模的求法以及一元二次不等式的解法,是基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.
如图,曲线C1是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的一部分,F1,F2是其两焦点.曲线C2是以原点O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的一个公共点,并且∠AF2F1为钝角.我们把由曲线C1和C2合成的曲线C称为“月食圆”.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
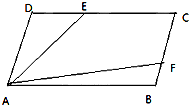 在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.
在平行四边形ABCD中,已知$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,E、F分别是边CD和BC上的点,满足$\overrightarrow{DC}$=3$\overrightarrow{DE}$,$\overrightarrow{BC}$=3$\overrightarrow{BF}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤1} | B. | {x|1≤x<2} | C. | {x|-1<x≤0} | D. | {x|0≤x<1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
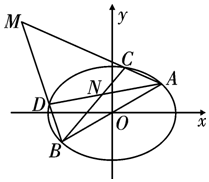 如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点A($\sqrt{2}$,1)是椭圆上的一点,且椭圆C的离心率为$\frac{{\sqrt{2}}}{2}$,直线AO与椭圆C交于点B,且C,D是椭圆上异于A,B的任意两点,直线AC,BD相交于点M,直线AD,BC相交于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com