
 为奇函数,满足f(1)<f(3),且不等式0≤f(x)≤
为奇函数,满足f(1)<f(3),且不等式0≤f(x)≤ 的解集是[-2,-1]∪[2,4].
的解集是[-2,-1]∪[2,4]. 都成立,求实数m的取值范围.
都成立,求实数m的取值范围. 为奇函数∴
为奇函数∴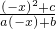 =-
=- ,解得b=0.…(2分)
,解得b=0.…(2分) 的解集中包含2和-2,
的解集中包含2和-2,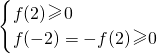
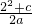 ,所以c=-4 …(4分)
,所以c=-4 …(4分) ,f(3)=-
,f(3)=-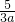 ,
, <
<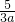 ,所以a>0…(5分)
,所以a>0…(5分)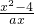 是增函数.
是增函数.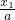 -
-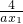 -
-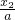 +
+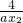 =
= (x1-x2)(1+
(x1-x2)(1+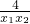 )<0
)<0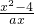 是增函数.
是增函数. =
=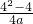 ,解得a=2.
,解得a=2.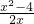 …(7分)
…(7分) 为奇函数∴f(x)=
为奇函数∴f(x)= 在(-∞,0)上也是增函数.…(8分)
在(-∞,0)上也是增函数.…(8分) …(10分)
…(10分) ≥
≥ …(12分)
…(12分) 对一切θ∈R成立.…(13分)
对一切θ∈R成立.…(13分) 的解集中包含2和-2,可得,f(2)≥0,
的解集中包含2和-2,可得,f(2)≥0, ,f(3)=-
,f(3)=-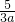 ,即-
,即- <
<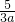 ,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=
,从而可求a的范围,利用函数单调性的定义证明在a>0时,在(0,+∞)上f(x)=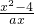 是增函数.由f(4)=
是增函数.由f(4)= =
=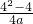 可求a
可求a 为奇函数可得f(x)=
为奇函数可得f(x)= 在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)=
在(-∞,0)上也是增函数,结合-3≤-2+sinθ≤-1,可得f(-3)≤f(-2+sinθ)≤f(-1)= ,从而可得m的取值范围
,从而可得m的取值范围

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| 1 |
| x |
| x+f(x) |
| xe2x |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com