
【题目】已知z∈C,z+2i 和 ![]() 都是实数.
都是实数.
(1)求复数z;
(2)若复数(z+ai)2 在复平面上对应的点在第四象限,求实数a 的取值范围.
【答案】
(1)解:设z=a+bi(a,b∈R),则z+2i=a+(b+2)i,
![]() ,
,
∵z+2i 和 ![]() 都是实数,∴
都是实数,∴ 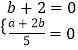 ,解得
,解得 ![]() ,∴z=4﹣2i
,∴z=4﹣2i
(2)解:由(1)知z=4﹣2i,∴(z+ai)2=[4+(a﹣2)i]2=16﹣(a﹣2)2+8(a﹣2)i,
∵(z+ai)2 在复平面上对应的点在第四象限,∴ ![]() ,
,
即 ![]() ,∴
,∴ ![]() ,∴﹣2<a<2,即实数a 的取值范围是(﹣2,2).
,∴﹣2<a<2,即实数a 的取值范围是(﹣2,2).
【解析】(1)化简等式,利用复数为实数的条件求出a,b的值,即得复数z.(2)化简式子,利用复数与复平面内对应点之间的关系列出不等式组,解不等式组求得实数a 的取值范围.
【考点精析】关于本题考查的复数的定义,需要了解形如![]() 的数叫做复数,
的数叫做复数,![]() 和
和![]() 分别叫它的实部和虚部才能得出正确答案.
分别叫它的实部和虚部才能得出正确答案.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱ABC﹣A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC= ![]() ,点O为AC的中点.
,点O为AC的中点. 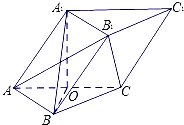
(1)求证:AC⊥平面A1OB;
(2)求二面角B1﹣AC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 上的点,
上的点, ![]() ,
, ![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() ,设
,设![]() ,试确定
,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,
(1)若命题p为真命题,求实数m的取值范围;
(2)若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市2017年3月1日至16日的空气质量指数趋势图,空气质量指数![]() 小于
小于![]() 表示空气质量优良,空气质量指数大于
表示空气质量优良,空气质量指数大于![]() 表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
表示空气重度污染,某人随机选择3月1日至3月14日中的某一天到达该市.
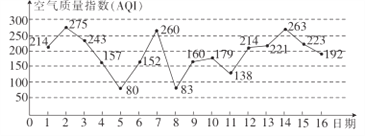
(1)若该人到达后停留![]() 天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
天(到达当日算1天),求此人停留期间空气质量都是重度污染的概率;
(2)若该人到达后停留3天(到达当日算1天〉,设![]() 是此人停留期间空气重度污染的天数,求
是此人停留期间空气重度污染的天数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln(2x+1)+bx+1.
(1)若函数y=f(x)在x=1处取得极值,且曲线y=f(x)在点(0,f(0))处的切线与直线2x+y﹣3=0平行,求a的值;
(2)若 ![]() ,试讨论函数y=f(x)的单调性.
,试讨论函数y=f(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数fn(x)= ![]() x3﹣
x3﹣ ![]() (n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(n+1)x2+x(n∈N*),数列{an}满足an+1=f'n(an),a1=3.
(1)求a2 , a3 , a4;
(2)根据(1)猜想数列{an}的通项公式,并用数学归纳法证明;
(3)求证: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com