
[2012·上海卷] 如图1-1,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=![]() ,AB=2,AC=2
,AB=2,AC=2![]() ,PA=2,求:
,PA=2,求:
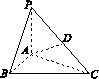
图1-1
(1)三棱锥P-ABC的体积;
(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示).
科目:高中数学 来源: 题型:
[2012·上海卷] 如图1-1,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=![]() ,AB=2,AC=2
,AB=2,AC=2![]() ,PA=2,求:
,PA=2,求:
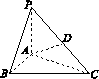
图1-1
(1)三棱锥P-ABC的体积;
(2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考上海卷理科21)(6+8=14分)海事救援船对一艘失事船进行定位:以失事船的当前位置为原点,以正北方向为![]() 轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里
轴正方向建立平面直角坐标系(以1海里为单位长度),则救援船恰好在失事船正南方向12海里![]() 处,如图.现假设:①失事船的移动路径可视为抛物线
处,如图.现假设:①失事船的移动路径可视为抛物线![]() ;②定位后救援船即刻沿直线匀速前往救援;③救援船出发
;②定位后救援船即刻沿直线匀速前往救援;③救援船出发![]() 小时后,失事船所在位置的横坐标为
小时后,失事船所在位置的横坐标为![]() .
.
(1)当![]() 时,写出失事船所在位置
时,写出失事船所在位置![]() 的纵坐标.若此时两船恰好会合,求
的纵坐标.若此时两船恰好会合,求
救援船速度的大小和方向;
(2)问救援船的时速至少是多少海里才能追上失事船?
查看答案和解析>>
科目:高中数学 来源: 题型:
(2012年高考上海卷理科22)(4+6+6=16分)在平面直角坐标系![]() 中,已知双曲线
中,已知双曲线![]() :
:![]() .
.
(1)过![]() 的左顶点引
的左顶点引![]() 的一条渐进线的平行线,求该直线与另一条渐进线及
的一条渐进线的平行线,求该直线与另一条渐进线及![]() 轴围成的三角形的面积;
轴围成的三角形的面积;
(2)设斜率为1的直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,若
两点,若![]() 与圆
与圆![]() 相切,求证:
相切,求证:![]() ;
;
(3)设椭圆![]() :
:![]() ,若
,若![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的动点,且
上的动点,且![]() ,求证:
,求证:![]() 到直线
到直线![]() 的距离是定值.
的距离是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com