
【题目】设函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() ,若
,若![]() 在
在![]() 上恒成立,求a的取值范围.
上恒成立,求a的取值范围.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单递增;当
上单递增;当![]() 时,
时,![]() 在
在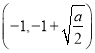 上单调递减,
上单调递减,![]() 在
在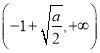 上单调递增;(2)
上单调递增;(2)![]()
【解析】
(1)求导,对参数进行分类讨论,根据导数的正负即可容易判断函数单调性;
(2)对参数进行分类讨论,根据函数的单调性,结合函数的最值,即可求得结果.
(1)![]() 定义域为
定义域为![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 在
在![]() 上单递增;
上单递增;
当![]() 时,令
时,令![]() 得
得![]() 或
或![]() (舍去)
(舍去)
当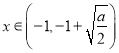 时,
时,![]() ,此时
,此时![]() 单调递减
单调递减
当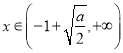 时,
时,![]() ,此时
,此时![]() 单调递增
单调递增
综上:当![]() 时,
时,![]() 在
在![]() 上单递增
上单递增
当![]() 时,
时,![]() 在
在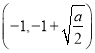 上单调递减
上单调递减
![]() 在
在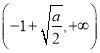 上单调递增
上单调递增
(2)由题意,![]() 在
在![]() 上恒成立.
上恒成立.
①若![]() ,
,![]()
![]()
![]()
令![]() ,
,![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() 成立,
成立,
故![]() 时,
时,![]() 成立.
成立.
②若![]() 时,令
时,令![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增
上单调递增![]() ﹐即有
﹐即有![]() .
.
![]() ,即
,即![]()
要使![]() 成立,必有
成立,必有![]() 成立.
成立.
由(1)可知,![]() 时,
时,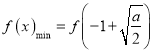 ,又
,又![]() ,
,
则必有![]() ,得
,得![]() .
.
此时,
![]()
![]()
令![]()
![]()
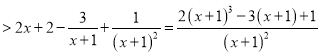
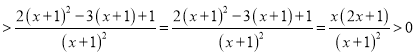
即![]() 恒成立,故
恒成立,故![]() 在
在![]() 上单调递增,
上单调递增,![]()
故![]() 时,
时,![]() 成立.
成立.
综上,a的取值范围是![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】为了解某地中小学生的近视形成原因,教育部门委托医疗机构对该地所有中小学生的视力做了一次普查.现该地中小学生人数和普查得到的近视情况分别如图1和图2所示.
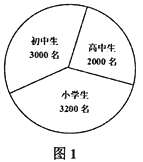
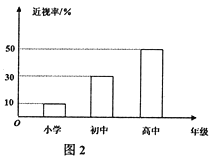
(1)求该地中小学生的平均近视率(保留两位有效数字);
(2)为调查中学生用眼卫生习惯,该地用分层抽样的方法从所有初中生和高中生中确定5人进行问卷调查,再从这5人中随机选取2人继续访谈,则此2人全部来自高中年级的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区有3个不同值班地点,每个值班地点需配一名医务人员和两名警察,现将3名医务人员(1男2女)和6名警察(4男2女)分配到这3个地点去值班,要求每个值班地点至少有一名女性,则共有______种不同分配方案.(用具体数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为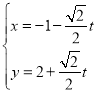 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019冠状病毒病(CoronaVirus Disease2019(COVID-19))是由新型冠状病毒(2019-nCoV)引发的疾病,目前全球感染者以百万计,我国在党中央、国务院、中央军委的坚强领导下,已经率先控制住疫情,但目前疫情防控形势依然严峻,湖北省中小学依然延期开学,所有学生按照停课不停学的要求,居家学习.小李同学在居家学习期间,从网上购买了一套高考数学冲刺模拟试卷,快递员计划在下午4:00~5:00之间送货到小区门口的快递柜中,小李同学父亲参加防疫志愿服务,按规定,他换班回家的时间在下午4:30~5:00,则小李父亲收到试卷无需等待的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某大型厂区有三个值班室![]() ,值班室
,值班室![]() 在值班室
在值班室![]() 的正北方向
的正北方向![]() 千米处,值班室
千米处,值班室![]() 在值班室
在值班室![]() 的正东方向
的正东方向![]() 千米处.
千米处.
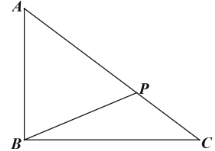
(1)保安甲沿![]() 从值班室
从值班室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的距离;
的距离;
(2)保安甲沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,保安乙沿
,保安乙沿![]() 从值班室
从值班室![]() 出发前往值班室
出发前往值班室![]() ,甲乙同时出发,甲的速度为
,甲乙同时出发,甲的速度为![]() 千米/小时,乙的速度为
千米/小时,乙的速度为![]() 千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为
千米/小时,若甲乙两人通过对讲机联系,对讲机在厂区内的最大通话距离为![]() 千米(含
千米(含![]() 千米),试问有多长时间两人不能通话?
千米),试问有多长时间两人不能通话?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”.
调查结果如下:
0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 | |
理科生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
文科生(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)完成如下![]() 列表,并判断是否由
列表,并判断是否由![]() 的把握认为.了解阿基米德与选择文理科有关?
的把握认为.了解阿基米德与选择文理科有关?
比较了解 | 不太了解 | 合计 | |
理科生 | p> | ||
文科生 | |||
合计 |
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(i)求抽取的文科生和理科生的人数;
(ii)从10人的样本中随机抽取两人,求两人都是文科生的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com