
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 存在两个极值点
存在两个极值点![]() ,且关于
,且关于![]() 的方程
的方程![]() 恰有三个实数根
恰有三个实数根![]() ,
,![]() ,
,![]()
![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)求导后按照![]() 、
、![]() 、
、![]() 分类讨论,求出
分类讨论,求出![]() 、
、![]() 的解集即可得解;
的解集即可得解;
(2)构造新函数![]() ,求导后可得
,求导后可得![]() 即可得
即可得![]() ;同理可得
;同理可得![]() ,即可得证.
,即可得证.
(1)由题意得![]() ,
,
令![]() 即
即![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,
时,![]() ,
,
![]() 的两根为
的两根为![]() ,
,![]() ,
,
(i)当![]() 即
即![]() 时,
时,![]() ,
,
所以当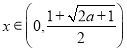 时,
时,![]() ;当
;当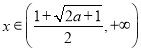 时,
时,![]() ;
;
所以![]() 在
在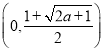 上单调递减,
上单调递减,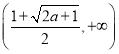 单调递增;
单调递增;
(ii)当![]() 即
即![]() 时,
时,![]() ,
,
所以当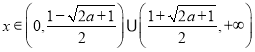 时,
时,![]() ;
;
当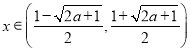 时,
时,![]() ;
;
则![]() 在
在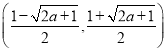 上单调递减,在
上单调递减,在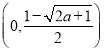 ,
,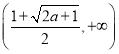 单调递增.
单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在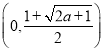 上单调递减,
上单调递减,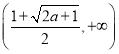 单调递增;当
单调递增;当![]() 时,
时,![]() 在
在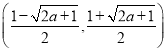 上单调递减,
上单调递减,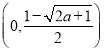 ,
,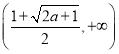 单调递增;
单调递增;
(2)证明:由题意得![]() ,
,![]() ,
,![]() ,
,
令![]() ,
,
则![]()
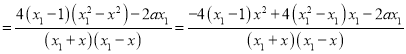 ,
,
由(1)知![]() ,
,
则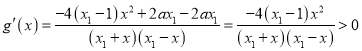
又![]() ,可知对于
,可知对于![]() 均有
均有![]() ,
,
所以![]() ,所以
,所以![]() ,
,
由![]() 可得
可得![]() ,
,
结合函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 即
即![]() ,
,
令![]() ,
,
同理可得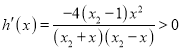 ,
,
由![]() 可得当
可得当![]() 时,
时,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
由![]() 可得
可得![]() ,
,
结合函数![]() 在
在![]() 上单调递增,可得
上单调递增,可得![]() 即
即![]() ,
,
所以![]() 即
即![]() ,得证.
,得证.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱中![]() ,它的体积是
,它的体积是![]() 底面△ABC中,∠BAC=90°,AB=4,AC=3,
底面△ABC中,∠BAC=90°,AB=4,AC=3,![]() 在底面的射影是D,且D为BC的中点.
在底面的射影是D,且D为BC的中点.
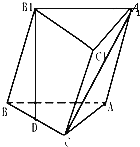
(1)求侧棱![]() 与底面ABC所成角的大小;
与底面ABC所成角的大小;
(2)求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,点
的左焦点为F,点![]() ,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
,过M的直线与椭圆E交于A,B两点,线段AB中点为C,设椭圆E在A,B两点处的切线相交于点P,O为坐标原点.
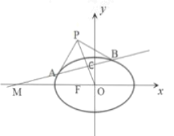
(1)证明:O、C、P三点共线;
(2)已知![]() 是抛物线
是抛物线![]() 的弦,所在直线过该抛物线的准线与y轴的交点,
的弦,所在直线过该抛物线的准线与y轴的交点,![]() 是弦
是弦![]() 在两端点处的切线的交点,小明同学猜想:
在两端点处的切线的交点,小明同学猜想:![]() 在定直线上.你认为小明猜想合理吗?若合理,请写出
在定直线上.你认为小明猜想合理吗?若合理,请写出![]() 所在直线方程;若不合理,请说明理由.
所在直线方程;若不合理,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,数列
,数列![]() 中的每一项均在集合
中的每一项均在集合![]() 中,且任意两项不相等,又对于任意的整数
中,且任意两项不相等,又对于任意的整数![]() ,均有
,均有![]() .例如
.例如![]() 时,数列
时,数列![]() 为
为![]() 或
或![]() .
.
(1)当![]() 时,试求满足条件的数列
时,试求满足条件的数列![]() 的个数;
的个数;
(2)当![]() ,求所有满足条件的数列
,求所有满足条件的数列![]() 的个数.
的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类:可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由10位同学组成四个宣传小组,其中可回收物与餐厨垃圾宣传小组各有2位同学,有害垃圾与其他垃圾宣传小组各有3位同学.现从这10位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com