
分析 (1)由$sinα=-\frac{5}{13},{sin^2}α+{cos^2}α=1$,即可得解${cos^2}α=\frac{144}{169}$,讨论α的范围,确定三角函数值的符号,利用同角三角函数基本关系式即可求值.
(2)原式分母用1=sin2α+cos2α代替,再利用同角三角函数基本关系式即可得解.
解答 解:(1)∵$sinα=-\frac{5}{13},{sin^2}α+{cos^2}α=1$,
∴${cos^2}α=\frac{144}{169}$,
若α第三象限角,则$cosα=-\frac{12}{13},tanα=\frac{sinα}{cosα}=\frac{5}{12}$,
若α第四象限角,则$cosα=\frac{12}{13},tanα=\frac{sinα}{cosα}=-\frac{5}{12}$.
(2)${sin^2}α+2sinαcosα=\frac{{{{sin}^2}α+2sinαcosα}}{{{{sin}^2}α+{{cos}^2}α}}=\frac{{{{tan}^2}α+2tanα}}{{{{tan}^2}α+1}}=\frac{8}{5}$.
点评 本题主要考查了同角三角函数基本关系式的应用,考查了计算能力和转化思想、分类讨论思想的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $3\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
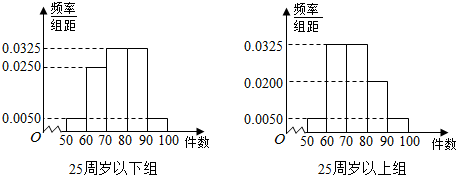
| P(K2≥k) | 0.100 | 0.010 | 0.001 |
| k | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\overrightarrow{e}$ | B. | -5$\overrightarrow{e}$ | C. | 23$\overrightarrow{e}$ | D. | -23$\overrightarrow{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com