(本小题共13分)
解:(Ⅰ)设圆O的半径为r,圆心为(0,0),
∵直线x-

y-4=0与圆O相切,
∴d=r=
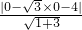
=2,…(3分)
则圆O的方程为x
2+y
2=4;…(5分)
(Ⅱ)在圆O上存在一点M,使得四边形OAMB为菱形,理由为:
法1:∵直线l:y=kx+3与圆O相交于A,B两点,
∴圆心O到直线l的距离d=
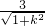
<r=2,
解得:k>

或k<-

,…(7分)
假设存在点M,使得四边形OAMB为菱形,…(8分)
则OM与AB互相垂直且平分,…(9分)
∴圆心O到直线l:y=kx+3的距离d=

|OM|=1,…(10分)
即d=
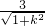
=1,整理得:k
2=8,…(11分)
解得:k=±2

,经验证满足条件,…(12分)
则存在点M,使得四边形OAMB为菱形;…(13分)
法2:记OM与AB交于点C(x
0,y
0),
∵直线l斜率为k,显然k≠0,
∴OM直线方程为y=-

x,…(7分)
将直线l与直线OM联立得:
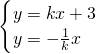
,
解得:
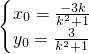
,
∴点M坐标为(
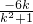
,
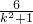
),…(9分)
又点M在圆上,将M坐标代入圆方程得:(
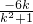
)
2+(
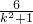
)
2=4,
解得:k
2=8,…(11分)
解得:k=±2

,经验证满足条件,…(12分)
则存在点M,使得四边形OAMB为菱形.…(13分)
分析:(Ⅰ)设圆O的半径为r,由圆心为原点(0,0),根据已知直线与圆O相切,得到圆心到直线的距离d=r,利用点到直线的距离公式求出圆心O到已知直线的距离d,即为圆的半径r,由圆心和半径写出圆O的标准方程即可;
(Ⅱ)在圆O上存在一点M,使得四边形OAMB为菱形.理由为:
法1:由直线l与圆O相交,得到圆心到直线l的距离d小于圆的半径r,利用关于k的不等式,求出不等式的解集得到k的范围,假设存在点M,使得四边形OAMB为菱形,利用菱形的性质得到对角线OM与AB垂直且平分,可得出圆心O到直线l的距离d等于|OM|的一半,即为半径的一半,根据半径求出d的值,列出关于k的方程,求出方程的解得到k的值,代入k范围中检验,满足条件,故存在点M,使得四边形OAMB为菱形;
法2:记OM与AB交于点C(x
0,y
0),由菱形的对角线互相垂直,根据直线l的斜率为k(k不为0),利用两直线垂直时斜率的乘积为-1求出直线OM的斜率,确定出直线OM的方程,将直线OM的方程与直线l方程联立组成方程组,求出方程组的解表示出x
0与y
0,确定出M的坐标,将M的坐标代入圆O的方程中,得到关于k的方程,求出方程的解得到k的值,经检验满足条件,故存在点M,使得四边形OAMB为菱形.
点评:此题考查了直线与圆相交的性质,直线与圆的位置关系,以及圆的标准方程,涉及的知识有:点到直线的距离公式,两直线的交点问题,菱形的性质,以及两直线垂直时斜率满足的关系,当直线与圆相切时,圆心到直线的距离等于圆的半径;当直线与圆相交时,圆心到直线的距离小于圆的半径;当直线与圆相离时,圆心到直线的距离大于圆的半径.

 相切.
相切. y-4=0与圆O相切,
y-4=0与圆O相切,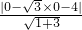 =2,…(3分)
=2,…(3分)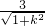 <r=2,
<r=2, 或k<-
或k<- ,…(7分)
,…(7分) |OM|=1,…(10分)
|OM|=1,…(10分)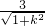 =1,整理得:k2=8,…(11分)
=1,整理得:k2=8,…(11分) ,经验证满足条件,…(12分)
,经验证满足条件,…(12分) x,…(7分)
x,…(7分)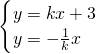 ,
,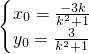 ,
,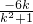 ,
,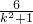 ),…(9分)
),…(9分)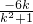 )2+(
)2+(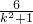 )2=4,
)2=4, ,经验证满足条件,…(12分)
,经验证满足条件,…(12分)
