
各项均为正数的数列 满足
满足 ,且
,且 是
是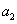 、
、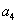 的等差中项.
的等差中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若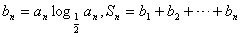 ,求使
,求使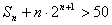 成立的n的最小.
成立的n的最小.
(I)先列出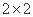 列联表
列联表
然后利用公式 ,计算出
,计算出 值,再根据k值是否大于6.635,来确定是不是有没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异.
值,再根据k值是否大于6.635,来确定是不是有没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异.
(II)先确定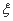 所有可能取值有0,1,2,3,然后求出每个值对应的概率,列出分布列,求出期望值.
所有可能取值有0,1,2,3,然后求出每个值对应的概率,列出分布列,求出期望值.
(Ⅰ)2乘2列联表
| 月收入不低于55百元人数 | 月收入低于55百元人数 | 合计 | |
| 赞成 |
|
| 32 |
| 不赞成 |
|
| 18 |
| 合计 | 10 | 40 | 50 |

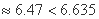
所以没有99%的把握认为月收入以5500为分界点对“楼市限购令”的态度有差异. ……(6分)
(Ⅱ)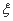 所有可能取值有0, 1,2,3,
所有可能取值有0, 1,2,3, ,
,
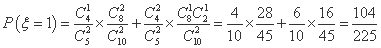

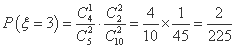
所以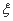 的分布列是
的分布列是
|
| 0 | 1 | 2 | 3 |
|
|
|
|
|
|
所以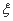 的期望值是
的期望值是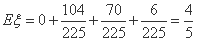 . …………………(12分)
. …………………(12分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
将 五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件
五种不同的文件随机地放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屈至多放一种文件,则文件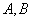 被放在相邻的抽屉内且文件
被放在相邻的抽屉内且文件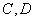 被放在不相邻的抽屉内的概率是 。
被放在不相邻的抽屉内的概率是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ex-1,g(x)=-x2+4x-3.若有f(a)=g(b),则b的取值范围为( ).
A.[2-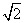 ,2+
,2+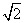 ] B.(2-
] B.(2-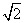 ,2+
,2+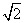 )
)
C.[1,3] D.(1,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
某班班会准备从甲、乙等7名学生中选派4名学生发言,要求甲、乙两名同学至少有一人参加且若甲、乙同时参加,则他们发言时不能相邻,那么不同的发言顺序的种数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
为了考察两个变量 和
和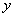 之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为
之间的线性相关性,甲、乙两位同学各自独立地做100次和150次试验,并且利用线性回归方法,求得回归直线分别为 和
和 ,已知两人在试验中发现对变量
,已知两人在试验中发现对变量 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量 的观测数据的平均值都是
的观测数据的平均值都是 ,那么下列说法正确的是( )
,那么下列说法正确的是( )
A. 和
和 有交点
有交点 B.
B. 与
与 相交,但交点不一定是
相交,但交点不一定是
C. 与
与 必定平行 D.
必定平行 D. 与
与 必定重合
必定重合
查看答案和解析>>
科目:高中数学 来源: 题型:
我们把离心率为e= 的双曲线
的双曲线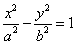 (a>0,b>0)称为黄金双曲线.如图,
(a>0,b>0)称为黄金双曲线.如图,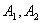 是双曲线
是双曲线
的实轴顶点,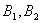 是虚轴的顶点,
是虚轴的顶点,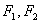 是左右焦点,
是左右焦点,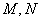 在双曲线上且过右焦点
在双曲线上且过右焦点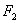 ,并且
,并且 轴,
轴,
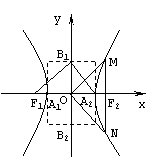 给出以下几个说法:
给出以下几个说法:
①双曲线x2-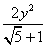 =1是黄金双曲线;
=1是黄金双曲线;
②若b2=ac,则该双曲线是黄金双曲线;
③如图,若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④如图,若∠MON=90°,则该双曲线是黄金双曲线.
其中正确的是( )
A.①②④ B.①②③ C.②③④ D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com