
分析 (1)由题意可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{3}}\\{\frac{{a}^{2}}{c}+c=10}\end{array}\right.$,解方程组得到a,c的值,结合隐含条件求得b,则椭圆方程可求;
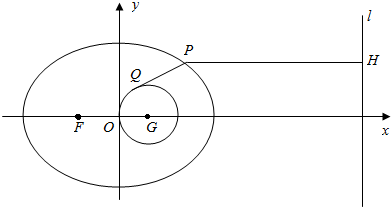
(2)圆G:(x-1)2+y2=1的圆心在椭圆的右焦点上,把$\frac{PQ}{PH}$转化为含椭圆离心率与PH的式子,求出PH的范围可得答案;
(3)设圆M:(x-m)2+(y-n)2=r2(r>0)满足条件,N(x,y),可知点(m,n)满足$\frac{{m}^{2}}{9}+\frac{{n}^{2}}{8}=1$,化圆的方程为一般式,由$\frac{NF}{NT}=\sqrt{2}$得x2+y2-6x-1=0,
代入圆的方程可得2(m-3)x+2ny-m2-n2-1+r2=0对圆M上点N(x,y)恒成立,由系数为0求得m,n,r的值,验证满足$\frac{{m}^{2}}{9}+\frac{{n}^{2}}{8}=1$后可得答案.
解答 解:(1)由题意可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{1}{3}}\\{\frac{{a}^{2}}{c}+c=10}\end{array}\right.$,解得a=3,c=1,∴b2=a2-c2=8.
则椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$;
(2)圆G:(x-1)2+y2=1的圆心在椭圆的右焦点上,
∴$(\frac{PQ}{PH})^{2}=\frac{P{G}^{2}-1}{P{H}^{2}}={e}^{2}-\frac{1}{P{H}^{2}}$,
∵e=$\frac{1}{3}$,PH∈[$\frac{{a}^{2}}{c}-a,\frac{{a}^{2}}{c}+a$]=[6,12],
∴$(\frac{PQ}{PH})^{2}∈$[$\frac{1}{12},\frac{15}{144}$],则$\frac{PQ}{PH}$∈[$\frac{\sqrt{3}}{6},\frac{\sqrt{15}}{12}$];
(3)设圆M:(x-m)2+(y-n)2=r2(r>0)满足条件,N(x,y),
其中点(m,n)满足$\frac{{m}^{2}}{9}+\frac{{n}^{2}}{8}=1$,则x2+y2=2mx+2ny-m2-n2+r2,
$NF=\sqrt{(x+1)^{2}+{y}^{2}},NT=\sqrt{(x-1)^{2}+{y}^{2}-{1}^{2}}$,
要使$\frac{NF}{NT}=\sqrt{2}$即NF2=2NT2,即x2+y2-6x-1=0,
代入x2+y2=2mx+2ny-m2-n2+r2,
得2(m-3)x+2ny-m2-n2-1+r2=0对圆M上点N(x,y)恒成立,
只要使$\left\{\begin{array}{l}{m-3=0}\\{n=0}\\{{r}^{2}={m}^{2}+{n}^{2}+1}\end{array}\right.$,得$\left\{\begin{array}{l}{m=3}\\{n=0}\\{{r}^{2}=10}\end{array}\right.$,经检验m=3,n=0满足$\frac{{m}^{2}}{9}+\frac{{n}^{2}}{8}=1$,
故存在以椭圆上点M为圆心的圆M,使得过圆M上任意一点N作圆G的切线(切点为T)
都满足$\frac{NF}{NT}=\sqrt{2}$,圆M的方程为(x-3)2+y2=10.
点评 本题考查椭圆的简单性质,考查了圆与圆锥曲线的位置关系,对于(3)的求解是该题的难点所在,与恒成立问题进行了交汇,试题设置难度较大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 圆 | C. | 抛物线 | D. | 线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com