练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    甲、乙、丙三人参加某次招聘会，假设甲能被聘用的概率是，甲、丙两人同时不能被聘用的概率是，乙、丙两人同时能被聘用的概率为，且三人各自能否被聘用相互独立.
    （1）求乙、丙两人各自被聘用的概率；
    （2）设为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值，求的分布列与均值（数学期望）.

    （1）乙、丙两人各自被聘用的概率分别为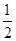、；（2）详见解析.

    解析试题分析：（1）分别设乙、丙两人各自被聘用的概率为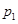、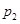，利用事件的独立性列出相应的方程进行求解，从而得出乙、丙两人各自被聘用的概率；（2）先列举出随机变量的可能取值，并根据事件的独立性求出在相应条件的概率，列出分布列并求出随机变量的均值（即数学期望）.
    试题解析：（1）设乙、丙两人各自被聘用的概率分别为、，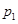
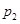    则甲、丙两人同时不能被聘用的概率是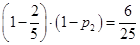，解得，
    乙、丙两人同时能被聘用的概率为，
    因此乙、丙两人各自被聘用的概率分别为、；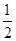
    （2）的可能取值有、，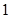
    则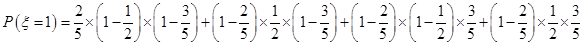
    ，
    ，
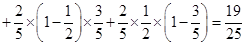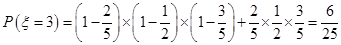    因此随机变量的分布列如下表所示







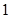
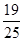
    所以随机变量的均值（即数学期望）.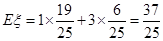
    考点：1.独立事件概率的计算；2.离散型随机变量的概率分布列与数学期望

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为合格.假设此人对A和B两种饮料没有鉴别能力.
    (1)求此人被评为优秀的概率;
    (2)求此人被评为良好及以上的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜)．进入总决赛的甲乙两队中，若每一场比赛甲队获胜的概率为，乙队获胜的概率为，假设每场比赛的结果互相独立．现已赛完两场，乙队以暂时领先．
    （1）求甲队获得这次比赛胜利的概率；
    （2）设比赛结束时两队比赛的场数为随机变量，求随机变量的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    在对某渔业产品的质量调研中，从甲、乙两地出产的该产品中各随机抽取10件，测量该产品中某种元素的含量（单位：毫克）.下表是测量数据的茎叶图：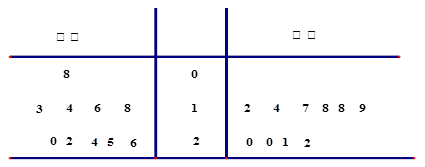

    规定：当产品中的此种元素含量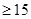毫克时为优质品.
    （1）试用上述样本数据估计甲、乙两地该产品的优质品率（优质品件数/总件数）；
    （2）从乙地抽出的上述10件产品中，随机抽取3件，求抽到的3件产品中优质品数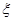的分布列及数学期望.

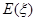    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某高校在202年自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[75，80)，第2组[80，85)， 第3组[85，90)，第4组[90，95)，第5组[95，100]得到的频率分布直方图如图所示．

    （1）分别求第3，4，5组的频率；
    （2）若该校决定在笔试成绩高的第3，4，5组中用分层抽样抽取6名学生进入第二轮面试，
    (ⅰ)已知学生甲和学生乙的成绩均在第三组，求学生甲和学生乙同时进入第二轮面试的概率；
    (ⅱ)学校决定在这6名学生中随机抽取2名学生接受考官D的面试，设第4组中有名学生被考官D面试，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆.

     
    		轿车A
    		轿车B
    		轿车C
    舒适型
    		100
    		150
    		z
    标准型
    		300
    		450
    		600
    （1）求z的值；
    （2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看作一个总体,从中任取一个分数.记这8辆轿车的得分的平均数为，定义事件{，且函数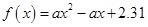没有零点}，求事件发生的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某工科院校对A，B两个专业的男女生人数进行调查，得到如下的列联表：

     
         		专业A
         		专业B
         		总计
     
    女生
         		12
         		4
         		16
     
    男生
         		38
         		46
         		84
     
    总计
         		50
         		50
         		100
     
    (1)从B专业的女生中随机抽取2名女生参加某项活动，其中女生甲被选到的概率是多少？
    (2)能否在犯错误的概率不超过0.05的前提下，认为工科院校中“性别”与“专业”有关系呢？
    注：K2＝
    P(K2≥k0)
         		0.25
         		0.15
         		0.10
         		0.05
         		0.025
     
    k0
         		1.323
         		2.072
         		2.706
         		3.841
         		5.024
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆

     
    		轿车A
    		轿车B
    		轿车C
    舒适型
    		100
    		150
    		z
    标准型
    		300
    		450
    		600
     
    （1）求下表中z的值；
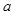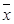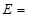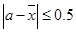    （2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下：94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数 记这8辆轿车的得分的平均数为，定义事件{，且函数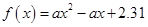没有零点}，求事件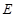发生的概率

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    “抛阶砖”是国外游乐场的典型游戏之一．参与者只须将手上的“金币”(设“金币”的半径为1)抛向离身边若干距离的阶砖平面上，抛出的“金币”若恰好落在任何一个阶砖(边长为2.1的正方形)的范围内(不与阶砖相连的线重叠)，便可获大奖.不少人被高额奖金所吸引，纷纷参与此游戏但很少有人得到奖品，请用所学的概率知识解释这是为什么．

    查看答案和解析>>

    同步练习册答案