
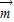 =(sinB,1-cosB),向量
=(sinB,1-cosB),向量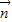 =(2,0),且
=(2,0),且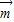 与
与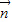 的夹角为
的夹角为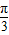 ,
,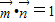 其中A,B,C是△ABC的内角.
其中A,B,C是△ABC的内角.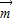 =(sinB,1-cosB),向量
=(sinB,1-cosB),向量 =(2,0),且
=(2,0),且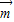 与
与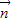 的夹角为
的夹角为 ,且
,且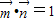 ,我们可以构造一个关于角B的三角方程,解方程后,即可求出一个关于B的三角函数,结合B的取值范围,即可求出B的大小;
,我们可以构造一个关于角B的三角方程,解方程后,即可求出一个关于B的三角函数,结合B的取值范围,即可求出B的大小;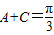 ,则sinA+sinC=
,则sinA+sinC=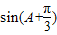 ,然后结合A的取值范围,根据正弦型函数的性质,我们即可求出sinA+sinC的取值范围
,然后结合A的取值范围,根据正弦型函数的性质,我们即可求出sinA+sinC的取值范围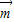 =(sinB,1-cosB)与向量
=(sinB,1-cosB)与向量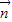 =(2,0)所成角为
=(2,0)所成角为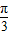 ,
,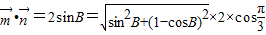 ,
,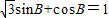 ,
,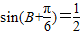

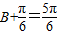
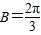 ;
;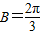 ,
,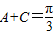
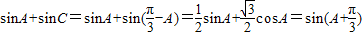
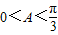 ,
, ,
,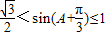 ,
,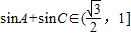 .
. 是向量中求夹角的唯一公式,要求大家熟练掌握.函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为-|A|,周期T=
是向量中求夹角的唯一公式,要求大家熟练掌握.函数y=Asin(ωx+φ)(A>0,ω>0)中,最大值或最小值由A确定,由周期由ω决定,即要求三角函数的周期与最值一般是要将其函数的解析式化为正弦型函数,再根据最大值为|A|,最小值为-|A|,周期T=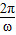 进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论.
进行求解.如果求其在区间上的值域和最值,则要结合图象进行讨论. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
| π |
| 3 |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| π |
| 6 |
| a+c |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com