
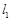 :
: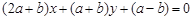 与直线
与直线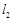 :
: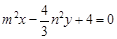 .
. 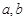 变化时,求证:直线
变化时,求证:直线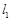 过定点,并求出这个定点的坐标;
过定点,并求出这个定点的坐标;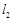 通过直线
通过直线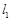 的定点,求点
的定点,求点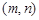 所在曲线
所在曲线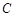 的方程;
的方程;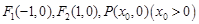 ,过点
,过点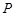 的直线交曲线
的直线交曲线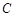 于
于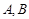 两点(
两点(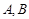 两点都在
两点都在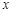 轴上方),且
轴上方),且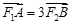 ,求此直线的方程.
,求此直线的方程.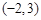 .(2)
.(2)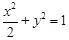 .(3)
.(3)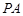 的方程为
的方程为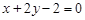 .
. 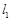 :
: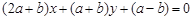 与直线
与直线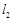 :
: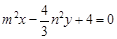 .
. 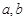 变化时,直线
变化时,直线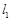 表示为过两条直线交点的直线系方程可知其过定点,并求出这个定点的坐标;
表示为过两条直线交点的直线系方程可知其过定点,并求出这个定点的坐标;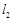 通过直线
通过直线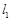 的定点,则可知点
的定点,则可知点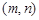 所在曲线
所在曲线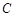 的方程;
的方程;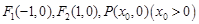 ,过点
,过点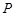 的直线交曲线
的直线交曲线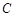 于
于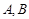 两点(
两点(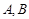 两点都在
两点都在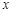 轴上方),且
轴上方),且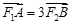 ,运用向量的共线的知识得到结论。
,运用向量的共线的知识得到结论。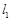 的方程化为
的方程化为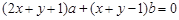 ,…………………………2分
,…………………………2分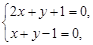 解得
解得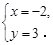 所以定点的坐标为
所以定点的坐标为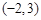 .………………4分
.………………4分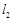 过定点
过定点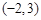 ,得
,得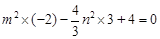 ,化简得
,化简得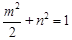 ,
,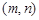 所在曲线
所在曲线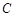 的方程为
的方程为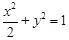 .……………………………………8分
.……………………………………8分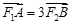 ,所以
,所以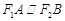 ,且
,且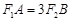 ,
, ,所以
,所以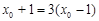 ,所以
,所以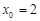 ,所以
,所以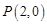 .…………10分
.…………10分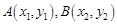 ,则
,则 ,
,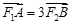 ,得
,得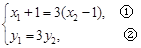 ,又由
,又由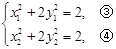
 所以
所以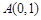 ,……………………………………………14分
,……………………………………………14分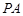 的方程为
的方程为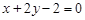 .……………………………………………………16分
.……………………………………………………16分

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com