
(本小题满分12分)设函数 .0
.0
(Ⅰ)求函数f(x)的单调区间和极值;
(Ⅱ)若对任意的 不等式| f′(x)|≤a恒成立,求a的取值范围.
不等式| f′(x)|≤a恒成立,求a的取值范围.
(Ⅰ)单调递增区间为(a,3a),单调递减区间为(-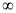 ,a)和(3a,+
,a)和(3a,+ ),
),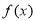 极小值=
极小值=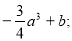
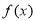 极小值=b.(Ⅱ)
极小值=b.(Ⅱ)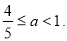
【解析】
试题分析:(Ⅰ)若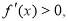 则函数在这个区间内为单调递增,若
则函数在这个区间内为单调递增,若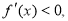 则函数在这个区间内为
则函数在这个区间内为
单调递减,若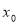 的左侧
的左侧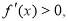 右侧
右侧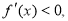 ,则
,则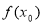 是极大值,若
是极大值,若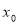 的左侧
的左侧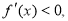 右侧
右侧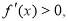 ,则
,则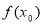 是极小值,求解即可;(Ⅱ)由|
是极小值,求解即可;(Ⅱ)由|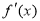 |≤a,得-a≤-x2+4ax-3a2≤a.根据不等式恒成立问题,则有
|≤a,得-a≤-x2+4ax-3a2≤a.根据不等式恒成立问题,则有 ,且
,且 ,再根据题意确定
,再根据题意确定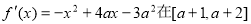 上是减函数.求出其最大值和最小值,构造不等式组
上是减函数.求出其最大值和最小值,构造不等式组
试题解析:(Ⅰ)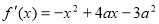 (1分)
(1分)
令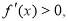 得
得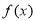 的单调递增区间为(a,3a)
的单调递增区间为(a,3a)
令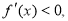 得
得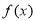 的单调递减区间为(-
的单调递减区间为(-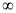 ,a)和(3a,+
,a)和(3a,+ ) (4分)
) (4分)
∴当x=a时,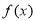 极小值=
极小值=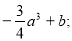
当x=3a时,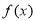 极小值=b. (6分)
极小值=b. (6分)
(Ⅱ)由|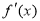 |≤a,得-a≤-x2+4ax-3a2≤a.①(7分)
|≤a,得-a≤-x2+4ax-3a2≤a.①(7分)
∵0<a<1,
∴a+1>2a.
∴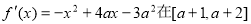 上是减函数. (9分)
上是减函数. (9分)
∴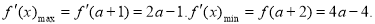
于是,对任意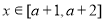 ,不等式①恒成立,等价于
,不等式①恒成立,等价于

又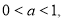 ∴
∴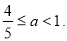
考点:1、函数的单调性与导数;2、函数的极值;3、不等式恒成立问题.


科目:高中数学 来源:[同步]2014年湘教版必修四 9.4分期付款问题中的有关计算练习卷(解析版) 题型:?????
(2013•郑州一模)把70个面包分5份给5个人,使每人所得成等差数列,且使较大的三份之和的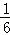 是较小的两份之和,问最小的1份为.( )
是较小的两份之和,问最小的1份为.( )
A.2 B.8 C.14 D.20
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省大同市高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知矩形ABCD的顶点在半径为13的球O的球面上,且AB=8,BC=6,则棱锥O-ABCD的高为
A.12 B.13 C.14 D.5
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊市高二上学期1月质量检测数学试卷(解析版) 题型:解答题
“ ”是“不等式
”是“不等式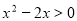 ”的( )
”的( )
A.充分不必要条件
B.充分必要条件
C.必要不充分条件
D.非充分必要条件
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第二段考文科数学卷(解析版) 题型:填空题
圆锥曲线中不同曲线的性质都是有一定联系的,比如圆可以看成特殊的椭圆,所以很多圆的性质结论可以类比到椭圆,例如;如图所示,椭圆C: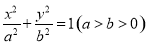 可以被认为由圆
可以被认为由圆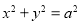 作纵向压缩变换或由圆
作纵向压缩变换或由圆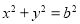 作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .
作横向拉伸变换得到的。依据上述论述我们可以推出椭圆C的面积公式为 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁沈阳东北育才学校高二上学期第二段考文科数学卷(解析版) 题型:选择题
已知双曲线 的两个焦点分别为
的两个焦点分别为 、
、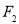 ,则满足
,则满足 的周长为
的周长为 的动点
的动点 的轨迹方程为
的轨迹方程为
A. B.
B. (
( )
)
C. D.
D. (
( )
)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上进教育名校学术联盟高三调研考试三文科数学试卷(解析版) 题型:选择题
如图,网格纸上校正方形的边长为1,且实线画出的是某多面体的三视图(第一个为正视图,下面的是侧视图),则该多面体的体积为( )
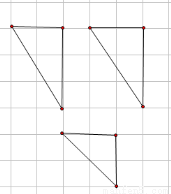
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com